Оглавление:
Некоторые приложения смешанного произведения
Определение взаимной ориентации векторов в пространстве
Определение взаимной ориентации векторов  ,
,  и
и  основано на следующих соображениях. Если
основано на следующих соображениях. Если 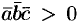 , то
, то  ,
,  ,
,  — правая тройка; если
— правая тройка; если 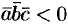 , то
, то  ,
,  ,
,  — левая тройка.
— левая тройка.
Установление компланарности векторов
Векторы  ,
,  и
и  компланарны тогда и только тогда, когда их смешанное произведение равно нулю (
компланарны тогда и только тогда, когда их смешанное произведение равно нулю (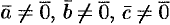 ):
):
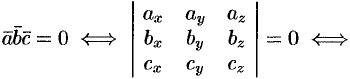 векторы
векторы  ,
,  ,
,  компланарны.
компланарны.
Определение объемов параллелепипеда и треугольной пирамиды
Нетрудно показать, что объем параллелепипеда, построенного на векторах  ,
,  и
и  вычисляется как
вычисляется как 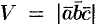 , а объем треугольной пирамиды, построенной на этих же векторах, равен
, а объем треугольной пирамиды, построенной на этих же векторах, равен 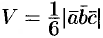 .
.
Пример №8.1.
Вершинами пирамиды служат точки 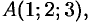
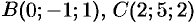 и
и 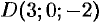 . Найти объем пирамиды.
. Найти объем пирамиды.
Решение:
Находим векторы  ,
,  ,
,  :
:
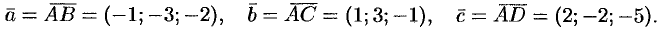
Находим 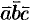 :
:
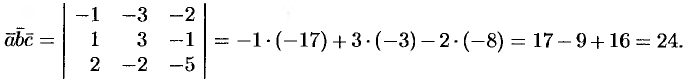
Следовательно, 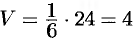 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Некоторые приложения векторного произведения |
| Выражение смешанного произведения через координаты |
| Параллельный перенос осей координат |
| Поворот осей координат |

