Оглавление:
Некоторые приложения поверхностного интеграла I рода
Приведем некоторые примеры применения поверхностного интеграла I рода.
Площадь поверхности
Если поверхность 
задана уравнением 
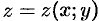, а ее проекция на плоскость 
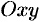есть область 
, в которо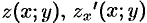й 
и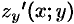 
— непрерывные функции, то ее площадь вычисляется по формуле
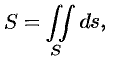
или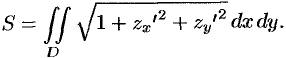 
Кроме того, поверхностный интеграл применяют для вычисления массы, координат центра масс, моментов инерции материальных поверхностей с известной поверхностной плотностью распределения массы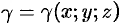 
. Все эти величины определяются одним и тем же способом: данную область разбивают на конечное число «мелких» частей, делая для каждой области деления упрощающие задачу предположения; находят приближенное значение искомой величины; переходят к пределу при неограниченном измельчении области деления. Проиллюстрируем описанный способ на примере определения массы материальной поверхности.
Масса поверхности
Пусть плотность распределения массы материальной поверхности есть 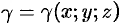. Для нахождения массы поверхности:
1. Разбиваем поверхность на 
частей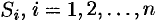 
, площадь которой обозначим 
.
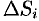2. Берем произвольную точку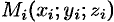 
в каждой области 
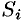. Предполагаем, что в пределах области 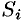плотность постоянна и равна значению ее в точке 
.
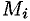3. Масса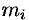 
области 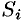мало отличается от массы 
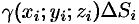фиктивной однородной области с постоянной плотностью
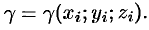
4. Суммируя 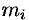по всей области, получаем: 
.
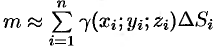5. За точное значение массы материальной поверхности принимается предел, к которому стремится полученное приближенное значение при стремлении к нулю диаметров областей 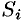, т. е.
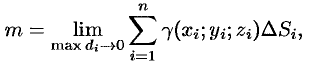
т. е.
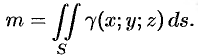
Моменты, центр тяжести поверхности
Статистические моменты, координаты центра тяжести, моменты инерции материальной поверхности находятся по соответствующим формулам:
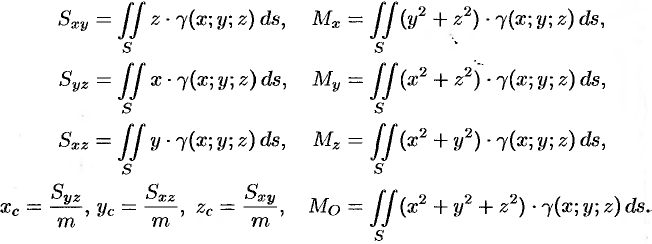
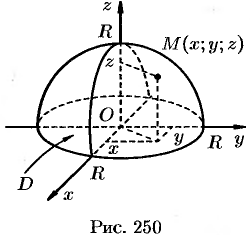
Пример №57.3.
Найти массу полусферы радиуса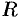 
, если в каждой точке поверхности плотность численно равна расстоянию этой точки от радиуса, перпендикулярного основанию полусферы.
Решение:
На рисунке 250 изображена полусфера радиуса 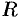. В уравнение 
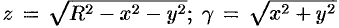— поверхностная плотность полусферы.
По формуле (57.7) находим:
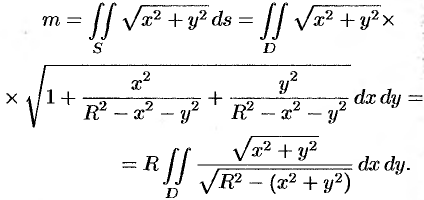
Переходим к полярным координатам:
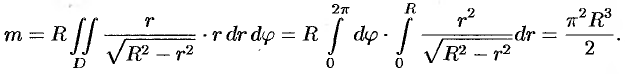
Внутренний интеграл вычислен с помощью подстановки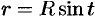 
:
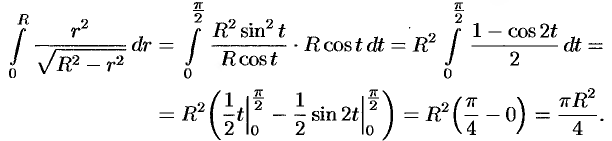
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Некоторые приложения криволинейного интеграла II рода |
| Вычисление поверхностного интеграла I рода |
| Вычисление поверхностного интеграла II рода |
| Некоторые приложения поверхностного интеграла II рода |
