Оглавление:
Некоторые приложения криволинейного интеграла I рода
Криволинейный интеграл I рода имеет разнообразные; приложения в математике и механике.
Длина кривой
Длина 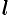 кривой
кривой  плоской или пространственной линии вычисляется по формуле
плоской или пространственной линии вычисляется по формуле 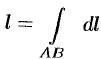 .
.
Площадь цилиндрической поверхности
Если направляющей цилиндрической поверхности служит кривая  , лежащая в плоскости
, лежащая в плоскости 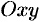 , а образующая параллельна оси
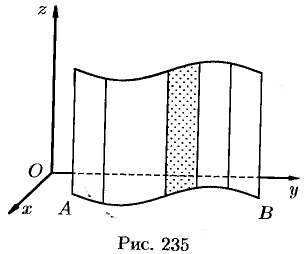
, а образующая параллельна оси 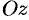 (см. рис. 235), то площадь поверхности, задаваемой функцией
(см. рис. 235), то площадь поверхности, задаваемой функцией  находится по формуле
находится по формуле 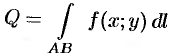 .
.
Масса кривой
Масса материальной кривой  (провод, цепь, трос,…) определяется формулой
(провод, цепь, трос,…) определяется формулой 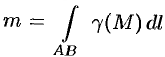 , где
, где 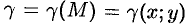 — плотность кривой в точке
— плотность кривой в точке  .
.
Разобьем кривую  на
на  элементарных дуг
элементарных дуг 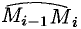
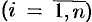 . Пусть
. Пусть 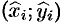 — произвольная точка дуги
— произвольная точка дуги 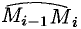 . Считая приближенно участок дуги однородным, т. е. считая, что плотность в каждой точке дуги такая же, как и в точке
. Считая приближенно участок дуги однородным, т. е. считая, что плотность в каждой точке дуги такая же, как и в точке 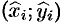 , найдем приближенное значение массы
, найдем приближенное значение массы 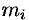 дуги
дуги 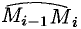 :
:
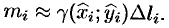
Суммируя, находим приближенное значение массы 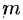 :
:
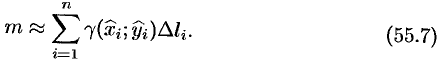
За массу кривой  примем предел суммы (55.7) при условии, что
примем предел суммы (55.7) при условии, что 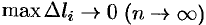 , т. е.
, т. е.
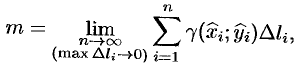
или, согласно формуле (55.2),
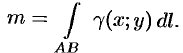
(Заметим, что предел существует, если кривая  гладкая, а плотность задана непрерывной в каждой точке
гладкая, а плотность задана непрерывной в каждой точке  функцией.)
функцией.)
Статические моменты, центр тяжести
Статические моменты относительно осей  и
и 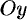 и координаты центра тяжести материальной кривой
и координаты центра тяжести материальной кривой  определяются по формулам
определяются по формулам
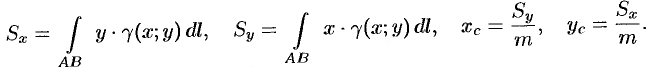
Моменты инерции
Для материальной кривой  моменты
моменты 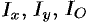 инерции относительно осей
инерции относительно осей  ,
,  и начала координат соответственно равны:
и начала координат соответственно равны:
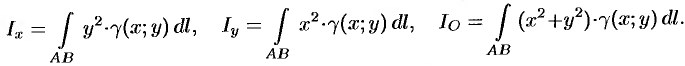
Пример №55.3.
Найти центр тяжести полуокружности 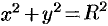 , лежащей в верхней полуплоскости. Плотность считать равной единице в каждой точке кривой (
, лежащей в верхней полуплоскости. Плотность считать равной единице в каждой точке кривой (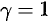 ).
).
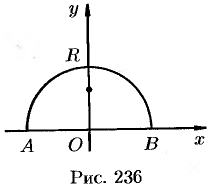
Решение:
Из соображений симметрии ясно, что центр тяжести находится на оси 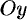 (см. рис. 236). Поэтому
(см. рис. 236). Поэтому 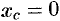 . Ордината центра тяжести
. Ордината центра тяжести
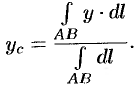
Знаменатель дроби — длина полуокружности. Поэтому 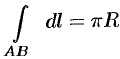 .
.
Для вычисления числителя воспользуемся параметрическими уравнениями окружности 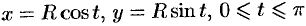 . Имеем:
. Имеем:
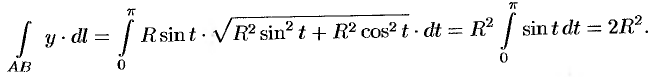
Следовательно, 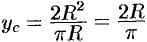 . Итак,
. Итак, 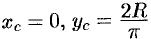 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Некоторые приложения тройного интеграла |
| Вычисление криволинейного интеграла I рода |
| Вычисление криволинейного интеграла II рода |
| Формула Остроградского-Грина |

