Некоторые теоремы о квадратичных иррациональностях

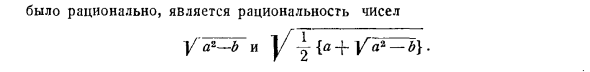
Некоторые теоремы о квадратичных иррациональностях

• Некоторые теоремы о иррациональности второго порядка. Два чистых иррациональных числа второго порядка называются подобными, если они являются рациональными кратными одной иррациональности. так / 8 = 2/2, 1 = 4/2, Следовательно, это та же иррациональность, что и / 8. С другой стороны, если и и-являются положительными непересекающимися числами, и ни одно из них не является целым квадратом, то и и / jV не являются одинаковой иррациональностью. Конечно, / M =? Я VN-iV *.

В этом случае y / MN, очевидно, является рациональным числом, и поэтому (см. Пример II.3), _ является целым числом. Следовательно, ASh = P-}, где P — целое число. Пусть a, b, c, … — простые делители числа Py, MN = awb * 9c * 4 Где a, (3, 7, … — натуральные числа. MN делится на «. M делится на a2a или N делится на aia1. И M, и TV делятся на aa

Где все символы представляют собой целые числа. Людмила Фирмаль

Поскольку M и N взаимно просты по предположению, эту возможность следует отбросить, так как эти рассуждения применимы к каждому фактору b * RU …, M является частью этих факторов, а N Должны быть разделены на другие факторы, то M = Pl N = Pl Где P \ — произведение нескольких факторов ai C, D разумны, A + y ‘B = C + / D, A = C и B = D, или B и D — квадраты рациональных чисел соответственно. На самом деле, B-D разумно, / B— / B = C — A Это также разумно. Если B не равно D (иначе A также равно C), / B + / D = (B-D) / (/ B- / D) Это также разумно. Следовательно, \ B и \ fD разумны. Результат. Если A + _ / ~ B = _C + / D, A- / B = C- \ f D (если только yf B и \ f D не являются рациональными числами)

Пример VIII. 1. Докажите, что Y 2 и] / ~ 3 не похожи иррационально без применения результатов предыдущего параграфа. 2. Докажите, что Y a и \ P / a (где a разумно) аналогично неразумно (если не разумно). 3. Если a \ b является рациональным числом, ya \ ~ yb не является рациональным числом, если только Y a и Y b не являются рациональными числами. В случае af то же самое относится и к V ~ a-V ~ b.

• Решение задач по высшей математике

Алгебраические операции над действительными числами	Континуум
Квадратичные иррациональности	Непрерывное действительное переменное

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

• Если A 4-] / «B = aVC + VDt A = c И B = ■ D или A = D и B = C, или | A4, VT,} / 7> все разумные или подобные иррациональные. {Возведите в квадрат это соотношение и примените теорему из предыдущего абзаца. ] 5. Если Y b иррационально, ни (a — \ — Y b) gu, ни (i-Y b) b не является разумным. _ 6. Если x = p- \ ~ Y q (p и q — рациональные числа), докажите, что q; w (m — любое целое число) можно выразить в виде PQy q (P и Q — рациональные числа) , Например (P + Y ~? = Pr 4- + Y > (p + Y Y = p3 + 3PY + (3 + d) В результате любой полином + … + вверх С рациональным коэффициентом π0, …, an можно выразить в том же виде 7. Если b не является точным квадратом a- \ ~ Y b Если a b является корнем алгебраического уравнения с рациональным коэффициентом, то a-Y b также является корнем этого уравнения. 8. Send- *

Как показано в Примере 6. Умножение P + V I р числитель и знаменатель-я 9. Из примеров 6 и 8 выражение формы ^ к> G (x) и H (x) — это многочлены от n: рациональные коэффициенты, которые можно выразить в виде P + Oy. Где P и Q рациональны. 10. Если py q и pr-q положительны, VP ~) r YЯ можно выразить в виде Vx- \ ~ Vy. Здесь, 11. Найти условие Yp + y ~ q. Где р и д рациональны. Y x — \ — YyY можно использовать. Где x m y рационально. 12.

Необходимое и достаточное условие __, когда ag-b положителен V a + V к b + V a-V ‘Это было разумно, рациональность чисел Уж-б а] / — ^ {а-т Людмила Фирмаль