Оглавление:


Некоторые результаты решения дифференциальных уравнений сжимаемого ламинарного пограничного слоя
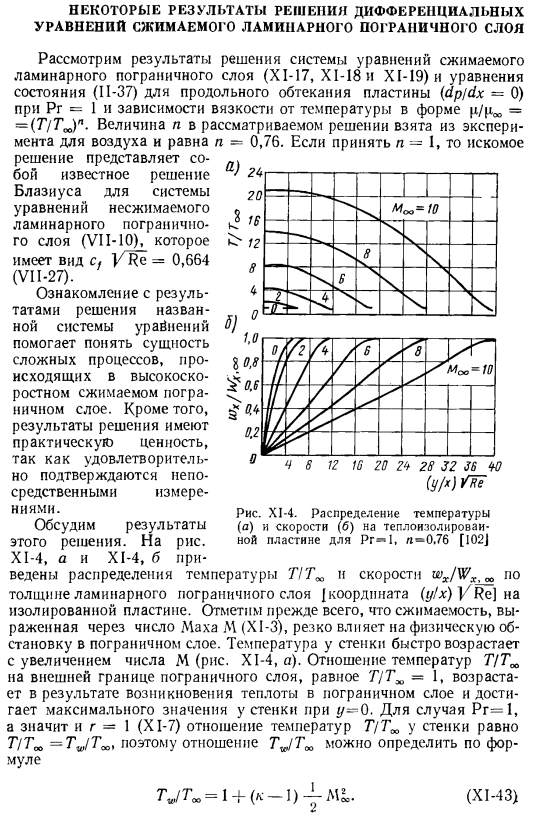
- Приведены результаты решения уравнений сжимаемого ламинарного пограничного слоя (XI-17, XI-18 и XI-19) и уравнения состояния (P-37) продольного обтекания пластины при Pr = 1 (dpjdx = 0)и p / p ^ = — (TlT ^ⁿ.Значение n для решения задачи взято из эксперимента с воздухом и равно n = 0,76.если вы получаете n-I, желательно Рисунок XI-4. Pr −1, α = 0,76 [i02j распределение температуры (a) и скорости (b) на изолирующей пластине Решение является известным решением Блазиуса системы уравнений несжимаемого ламинарного пограничного слоя (VII-10 ^form cf Re = 0.664 (VI1-27).
Знание результатов решения системы названных уравнений поможет понять суть сложных процессов, происходящих в высокоскоростном сжимаемом контуре layer. In кроме того, результаты решения имеют практическую ценность, так как они хорошо проверяются прямыми измерениями. Мы опишем последствия этого решения. Рис. XI-4, a и XI — 4, b на Показано распределение температуры TGG ^и скорости W /Wₓтогда толщина ламинарного пограничного слоя{координата (у/х) VxRe]на изолированной пластине.
Величина называется экстенсивной, если её значение для системы, сложенной из нескольких частей, равно сумме значений этой величины для каждой части. Людмила Фирмаль
Прежде всего, следует отметить, что сжимаемость, выраженная в числе Маха M(XI-3), существенно влияет на физическое состояние пограничного слоя. Температура вблизи стенки быстро возрастает с увеличением числа М(рис. Х1-4, а).Отношение температур T / Tl на внешней границе пограничного слоя, TjT ^ 1, Возраст- В результате появления тепла в пограничном слое, при y = 0 достигает максимального значения у стенки.
Для Pr = 1, следовательно r-1 (XI-7), отношение температуры T / Tm вблизи стенки равно T / T^=. таким образом, отношение T ^ TM можно определить следующим образом: Мул (ХІ-43) Эта формула показывает, как влияет степень сжатия К Температура стен. Для несжимаемых жидкостей со средней скоростью принимается M ^ = 0, тепло, выделяющееся в пограничном слое, игнорируется, и если T / T равно 1 на внешней границе пограничного слоя, то это соотношение не изменяется относительно поверхности адиабатической стенки (опорный рисунок X1-4, a, AC = 0).
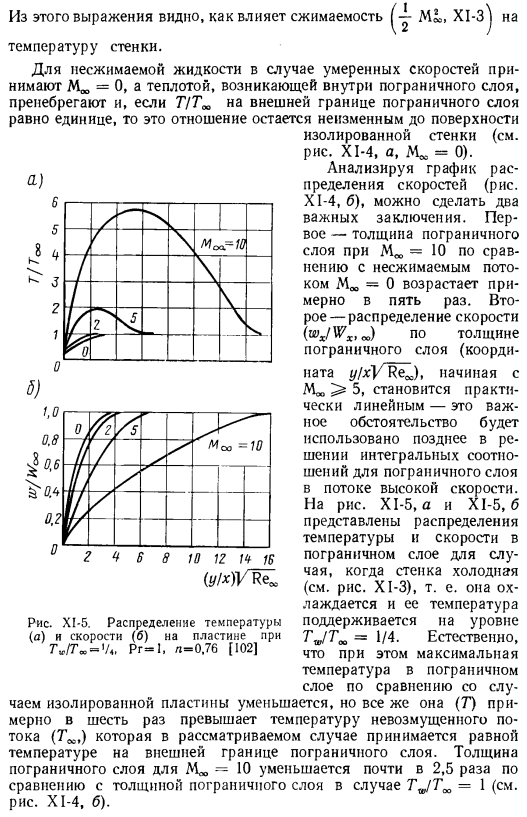
Рисунок Х5.Распределение температуры(d)и скорости (b) на пластине, ₀ 7 ′/ 7,₀ ’ / 4. Rg = 1, l = 0,76(1021 5.) Проанализировав график распределения скоростей (рис. XI-4, Б), можно сделать 2 важных вывода. Первая заключается в том, что толщина пограничного слоя при M»= 10 по сравнению с несжимаемым потоком Me,= 0 увеличивается примерно в 5 раз. 2-е-распределение скоростей по толщине пограничного слоя (wₓ / WₓₜC₀), причем координаты Y / XV начинаются с Re〜J, M»5) почти линейно-это важное обстоятельство в дальнейшем используется при решении интегрального соотношения пограничного слоя в быстром потоке.
На рис. XI-5, А и XI-5, б показано распределение температуры и скорости пограничного слоя при охлаждении стенки (см. рис. XI-3), то есть при ее охлаждении и поддержании ее температуры ТВ? ’«=1/4.Конечно.、 Самая высокая температура на границе в то же время По сравнению со случаем изолированной пластины слой уменьшается, но все же(T)примерно в 6 раз превышает температуру нестационарного течения (T^), которая в этом случае равна температуре внешней границы пограничного слоя.
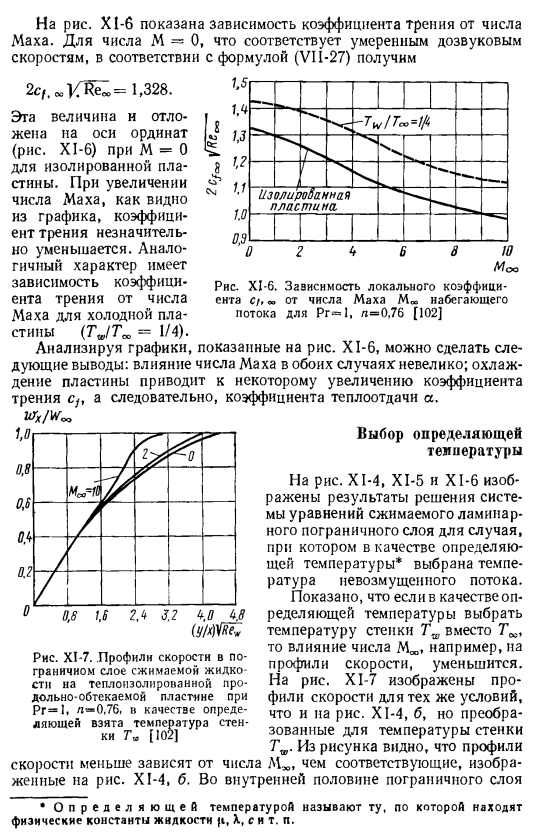
- Толщина пограничного слоя M, = 10 уменьшается почти в 2,5 раза по сравнению с толщиной пограничного слоя корпуса= 1(см. Рисунок XI-4, b). На рисунке Х1-6 показана зависимость коэффициента трения от числа Maha. In в соответствии с формулой (VI1-27), для числа M = 0, что соответствует умеренной дозвуковой 1,328. Это значение нанесено на ось ординат (рис. X1-6) при M = 0 на изолированном plate. As как видно из графика, коэффициент трения немного уменьшается по мере увеличения числа Маха.
Среди термодинамических величин выделяют экстенсивные (внутренняя энергия, энтропия, объём и др.) и интенсивные (давление, температура и др.) величины. Людмила Фирмаль
Зависимость коэффициента трения от числа Маха холодных пластин (TJT ^-1/4) имеет те же характеристики. 1,5. 0.3 ’—————————— 1 ———— O 2 b 6 8 10 МЭИ Рисунок XI-6. Зависимость локального коэффициента набегающего потока от Pr1, l = 0,76 a, o «числа Маха M» [102] Анализ графика, представленного на рисунке XI-6, позволяет сделать следующие выводы: влияние числа Маха в обоих случаях невелико. Охлаждение пластины незначительно увеличивает коэффициент трения Ср, что приводит к увеличению коэффициента теплопередачи A.
Рисунок XI-7. Pr = 1, профиль скорости пограничного слоя сжимаемой жидкости на изолированной продольно обтекаемой пластине 15 ~ 0,76.Температура стенки Т «[102]была принята в качестве решающей Определение выбор температуры На рисунках XI-4, XI-5 и XI-6 показан результат решения одновременных уравнений для сжимаемого ламинарного пограничного слоя при выборе температуры непертурбативного течения в качестве определяющей температуры. Например, если в качестве определяемой температуры выбрана температура стенки Tw, то показано, что влияние числа M «на профиль скорости уменьшается.
Рисунок XI-7 показан профиль скорости в том же состоянии, как показано на рисунке 7. Си-4, Б, но преобразован в температуры стенки Tст. Из рисунка видно, что профиль MF больше, чем соответствующий профиль, показанный на рисунке 1. XI-4, Б. внутренняя половина пограничного слоя Скорость не очень зависит от номера * Определяемая температура — это температура, при которой определяются физические константы жидкости p, X, c и т. д. Профиль скорости вообще не зависит от числа M*.
Это важное обстоятельство говорит о том, что можно подобрать определяемую температуру таким образом, чтобы показатель не оказывал существенного влияния на коэффициент трения и теплообмена. Поэтому для расчета сжимаемого пограничного слоя, если в качестве определяемой температуры выбрана соответствующая температура, можно использовать метод, разработанный для расчета несжимаемости.1 из этих методов будет рассмотрен в§ 4 настоящей главы.
Влияние числа Прандтля Pr на физическое состояние сжимаемого ламинарного пограничного слоя на пластине В приведенном выше примере рассмотрен результат решения системы уравнений пограничного слоя ПР-1.Решение в этом предположении интересно тем, что число прандлей в воздухе близко к 1.In кроме того, уравнение пограничного слоя при Pr = 1 значительно упрощается(например, сравнивая XI-22 и XI-23), а в некоторых случаях его можно интегрировать.
При Pr = 1 Известно, что толщина динамического и теплового пограничных слоев одинакова(Глава VII). Сравнение (VI1-8) и (VI1-34)、 Поэтому при PR 1 температурный пограничный слой толще динамического слоя. По мере увеличения числа Pr толщина динамического пограничного слоя увеличивается, а толщина теплового слоя уменьшается. Однако, если температура стенки Tw используется в качестве определяющей температуры ее структуры, то влияние числа Pr (или среднего значения Pr для газа) на профиль скорости будет small. It было подтверждено, что влияние числа Pg на коэффициент трения cₜ (PG умеренного значения для газа) также невелико.
Смотрите также:

