Оглавление:








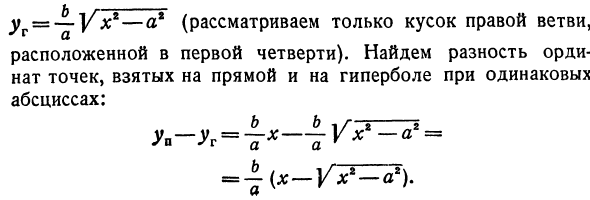

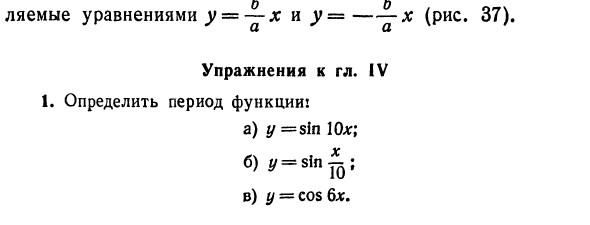


Некоторые простые неявные функции
- Некоторые простые неявные функции Подумай об уравнении Axf + 2 Bxu + C / + 2 Dx + 2 Eu + F = 0, (I) Коэффициенты A, B, C, D, E и F пронумерованы. Это уравнение можно решить для y. В результате выражения от y до x очень сложны. с того времени О, так рассуждения могут быть ограничены рассмотрением только первого квартала. В течение этого квартала с увеличением x увеличивается и значение y (рисунок 36). Кривая с координатами, где все точки удовлетворяют уравнению (3), называется гиперболой.
Благодаря симметрии гипербола имеет форму, показанную на рисунке. 37. Пересечение гиперболы и оси Ox называется вершиной гиперболы. Рисунок 37 Они имеют буквы А и А ^ «. Гиперболическая часть в первой и четвертой четвертях называется правой ветвью, а гиперболическая часть во второй и третьей четвертях называется левой ветвью. Рассмотрим линию, заданную уравнением y = —x. Указывает ординату точки на линии yn, чтобы ордината точки на этой линии не путалась с ординатой точки на гиперболе.
yrz = z ~ ‘\ / rx2-ar (учитывая только часть правой ветви, В первом квартале). Умножьте правую часть на x + Vx * –a2, чтобы разделить. = b (x- (x + V ^^ j x + V L ^ rz ^ или v _ v = b X * -Y (x * —ax) r = _ b_ x * —x * + a * Наконец При увеличении значения x правая часть уравнения (*) приближается к нулю.
Найти разность между ординатами точек на линии и гиперболой с той же абсциссой. Людмила Фирмаль
В результате разница ya-yt приближается к нулю. Другими словами, точки на прямой и гиперболе сближаются. Следовательно, рассматриваемая часть правой ветви гиперболы имеет вид Начало координат приближается к линии y = ~ x. Понятно, что из-за симметрии часть правой ветви, расположенная в четвертой четверти, приближается к прямой. Он определяется уравнением y = -x. Левая часть Филиал расположен в приближающемся втором квартале Прямая линия y = -jc, а левая часть ответвления б В третьей четверти линия у = -х.
Прямая, приближающаяся к бесконечности, когда гипербола покидает начало координат, называется гиперболической асимптотой. Таким образом, гипербола имеет две асимптоты,Он определяется уравнениями y = ~ x и y = —x (рис. 37). Практика ч. IV 1. Определите продолжительность функции. а) у = грех \ 0х; б) ^ = sinT5; в) у = COS 6 *.
- В каком направлении сдвинута синусоида y = sin (* + 5) относительно синусоиды i / = sin *? 3. В каком направлении синусоида r = sin (4 * -20) смещается относительно синусоиды y = slnx? 4. Как далеко синусоида y = sin 5×7 от оси Ox 5. Найдите тип и местоположение строки, определенной неявной функцией. а) 9lg1 + 16 ^ = 144; б) 9х2-16 г / * = 144; в) x * + 2 bxr + yy — 39 = 0. X1 и 1 6. Определить гиперболическую асимптоту =
Если мы находим x из выражения y из выражения (I), мы можем сказать, что выражение (I) определяет y как функцию от x. Это обычно выражается как: Уравнение (I) определяет y как неявную функцию от x. Например, выражение x2-f-d; 2 = 1 () определяет неявную функцию. Решая для вас, у = + V 1-x2 и () Следовательно, уравнение (), определяющее неявную функцию, фактически определяет функции gt (*) и (). В таких случаях уравнение () называется бинарной функцией. Вот некоторые конкретные случаи уравнения (I) и соответствующие геометрические диаграммы.
1. Окружность Подумай об уравнении
Если A = C = 1, B = D = E == 01 F = -R2, то его можно вывести из уравнения (1).
Подставляя ^ = ^ = 0 в формулу для выражения расстояния между двумя точками (глава 1 § 2 формулы (1)),Получите xr = x, y% = y, OQ = Yx1 + f.Из уравнения (1) V x2 + y-R, то есть OQ = /? Это означает, что все точки Q (x, y), координаты которых удовлетворяют уравнению (1), находятся на расстоянии R от начала координат. Аналогично, формула (x — a) 2 + + (Y — b) 2 = R * определяет окружность с радиусом R с центром в точке (a, b).
Следовательно, геометрическое положение точки, координаты которой удовлетворяют уравнению (1), представляет собой круг с радиусом R с центром в начале координат. Людмила Фирмаль
Пример 1. Найти уравнение для круга, равного радиусу 10 с центром в точке (2, 3). Предполагая, что a-2, b = -3 и x = 10, получим (x — r ^ + ^ + 3 ^ 10 Давайте решим это уравнение для y; 3 / = —3+ | / 100- (JC — 2) 2 у = -3- / 100- (х-2) 2. Первое из этих уравнений является уравнением верхней половины, а второе — уравнением нижней половины. 2. Подумайте об эллиптических уравнениях 5 + С-1. <2) Здесь a и b даны положительные числа. Решая с у в качестве ссылки, это делается следующим образом.
Это показывает, что уравнение (2) определяет две функции. Хотя абсолютное значение независимой переменной x меньше, чем a, радикальное представление положительно, а корень имеет два значения. Каждое значение x, удовлетворяющее неравенству, соответствует двум значениям ^, которые имеют одинаковое абсолютное значение.
Размер лютни Следовательно, геометрическое положение точки, определяемой уравнением (2), симметрично относительно оси Ox. Вы также можете проверить, что он симметричен относительно оси Oy. В результате мы ограничиваемся рассмотрением только первого квартала. x: = 0 y = b} для x = a y = 0. Также обратите внимание, что разница ar-x1 уменьшается с увеличением x. Следовательно, точка (xy y) перемещается из точки B (0, b) в нижний правый угол и достигает точки A (a, 0). По соображениям симметрии геометрическое расположение исследуемой точки является формой, показанной на рисунке. 34.
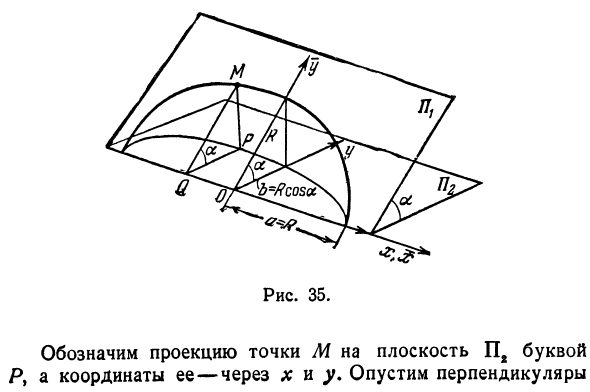
Результирующая линия называется эллипсом. Число 2a — это длина сегмента AgA, а число 26 — это длина сегмента Z ^ Z. ар — в бр Числа a и b называются полуосью эллипса. Номер — Эксцентриситет. Задание 1. Найдите проекцию круга на плоскость, которая не соответствует плоскости круга. Решения. Используйте две плоскости, которые пересекаются под углом а (рис. 35).
В каждом из этих самолетов В системе координат используйте * для оси Ox, чтобы получить прямую линию на пересечении плоскостей. Поэтому ось Ox является общей для обеих систем. Оси ординат различны, и их происхождение является общим для обеих систем. Хорошо — на самолете 34 со скоростью P 1 ворота с радиусом R По центру в начале координат уравнение имеет вид x * + y * = A * (). Поместите точку M (x> y) на эту окружность так, чтобы ее координаты удовлетворяли уравнению (). у. 1 1 дюйм * s O V —— __ 8,
Рисунок 35 Проекция точки M на плоскость представлена координатами a, x и y. Пропустить вертикальные линии От P и M до оси Ox это сегменты QP и QM. Треугольник PQM — это прямоугольник, в котором QP = y, QM = y, / _ PQM = a и, следовательно, y = QAf =. Точка абсциссы М и Р равны, то есть х = х. Подставить в уравнение (*) — В y = -3 — значение, тогда J cos a 1 X1 потому что Я U2 _ ха » 1 г ** » или £ l_i_ Y = я R * ‘(R cos a) *’
Это эллиптическое уравнение с полуосью a = R и ft = βcosa. Таким образом, эллипс — это проекция круга на плоскость, расположенную под углом к плоскости круга. Замечания. Вы можете думать о круге как о эллипсе с равными полуосями. 3. Рассмотрим гиперболическое уравнение Решение для ^ у дает две явные функции. Или одна двузначная функция В y = ± iVx2-a \
Функция y имеет действительное значение только в том случае, если x2 > = 0. Если χ> ar, каждому значению x соответствуют два значения y, поэтому кривая симметрична относительно оси Ox. Вы также можете увидеть симметрию вокруг оси
Смотрите также:
| Показательная функция | Примеры и определения |
| Логарифмическая функция | Область существования функции |

