Оглавление:


Некоторые общие свойства симметричных нелинейных сопротивлений
Некоторые общие характеристики симметричного нелинейного сопротивления. Нелинейный резистор с симметричными свойствами является одной из величин, определяющих состояние, то есть, если величина x функционирует в изменяющихся во времени условиях согласно закону x = x04-xt sinco / -Количество y-
- Следующие выводы: 1. Величина постоянной составляющей функции // (т.е. i / o)
зависит не только от величины x0, но и от величины x «r. Людмила Фирмаль
Это свойство выводится из формулы (9.17). y0 == a sh £ V0 (jfixm). 2. Кривая y = f (<o0, четные гармоники отображаются. Четные гармоники исчезают при x0 = 0.
Фаза четных гармоник зависит от знака постоянной составляющей (знак x0). 3. Изменяя значение x0 или y0, гармоники функции выше первой амплитуды </ (© 0. Первая из этих характеристик проиллюстрирована на рисунке.
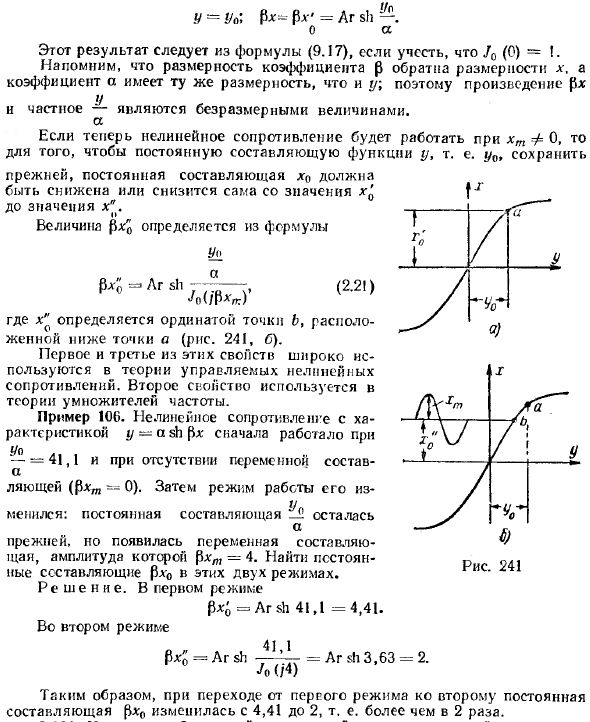
- Синусоидальная составляющая отсутствует (xm-0) Изображение этого процесса, касающееся характеристик нелинейного сопротивления, является точкой а (рис. 241 а). Y = Uy, ₽ * -₽l «= Ag sh-. Об этом результате Jo (0) =! Учитывается (9.17)!
Размерность коэффициента p является обратной величиной измерения x, а коэффициент a имеет то же измерение, что и y, поэтому
произведение p% y и частное являются безразмерными. Людмила Фирмаль
Напомним значение cc, где нелинейное сопротивление работает при xmΦ0, чтобы сохранить постоянную составляющую функции y, т.е. чтобы она оставалась постоянной, постоянная составляющая x0 — это значение x ^ Pxj должно быть уменьшено или уменьшено с x до x ^ определяется по формуле = Ar sh (2.21) * ´o (/ RAyag),
где x » — точка b ниже точки a (Рис. 241, б), первое и третье из этих свойств широко используются в теории управляемого нелинейного сопротивления. Второе свойство используется в теории умножителей частоты.
Пример 106. Нелинейное сопротивление -shРх характеристики у изначально работает с уо .., — = 41,1, без переменной составляющей (Рхш-0), затем изменен режим работы, постоянная составляющая такая же
Переменная компонента все еще видна, и ее амплитуда равна pxP1 = 4. Найдите постоянную составляющую px0 в этих двух режимах. Решение: в первом режиме Pxq = Ar sh 41.1 = 4.41. В режиме P * o = Ar sh = Ar sh 3.63 = 2. ч ( j4)
Поэтому при переходе из первого режима во второй режим постоянная составляющая px0 была изменена с 4.41 до 2. 2 раза.
Смотрите также:
| Переходные процессы в нелинейных цепях | Простейшие двухполюсники, их изображения в схемах цепей и уравнения |
| Магнитные цепи при постоянных потоках | Законы и уравнения Кирхгофа |

