Оглавление:


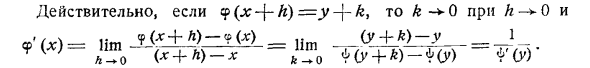
Некоторые общие правила дифференцирования
- Общие правила дифференциации. В следующей теореме функции f (x) и F (x) Производная от значения задачи f (x) и F ‘() (1) Если y (x) = f (x) — {- F (x) t, µ> (x) имеет производную 9 ‘(х) = F (х) + F’ (х). (2) 9 (x) = kf (x \, где k — постоянная, 9 (x) имеет производную (X) = kf (x). Эти результаты выводятся из общей теоремы примера XXXV. Оставьте 1 мг в качестве упражнения для читателя. (3)
- Если cp (x) = f (x) F (x), y (x) имеет производную ? «W = / Wf» (x) + f (x) F (x). конечно =] im f_ (x ± h) F (x + h) -f (x) F (x) = = m {f (x + h) + F (X)} = = f (x) F ‘(x) + F (x) f (x). (4) Если cf (x) = y ~ j и f (x) 0, mo 9 (x) имеет производную r {X) ~ {/ ()} ‘■ конечно (5) ((:):) — тки и F (jc) Φ0, mo 9 (x) имеет производную G (х) Я / / ‘(X) F (x) -f (x) F’ (x)
Это сразу следует (3) и (4). (6) Если от 9 (x) до F {f (x) \, то µ> (x) имеет производную 94 ) = ^ {/ ()} / »• Людмила Фирмаль
Необходимо соблюдать осторожность, чтобы доказать эту теорему 1). Установите f (x) = y, f (x — \ — ti) = y — \ — k, 0 равно 0, ■ {- • / <*). (!) Далее необходимо различать два случая. Предположим, что (a) / (x) и h малы, но не отличны от нуля. Тогда kzfz 0, (1) и o (x + h) -то ((x) _F (y + k) -F (y) — * — + F (y) f (x). (B)
| Обратные функции | Производные комплексных функций |
| Производные или дифференциальные коэффициенты | Обозначения дифференциального исчисления |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Предположим, что / (*) = 0 и h мало, но не отлично от нуля. Есть две возможности. Если £ = 0-> th — и Для к ^ тО, L h » & h Потому что первый элемент справа почти равен F ‘(y), а второй элемент мал -> — 0. В результате, — ^ — ^ — t ^ JZ ^ ifL мало во всех случаях Последняя теорема требует нескольких слов для предварительного объяснения.
Где Предположим, что> (Y) является функцией (см. §95), которая непрерывно увеличивается (или уменьшается) непрерывно в определенном диапазоне значений y. Тогда вы можете написать y = <p (x). Где 9 — функция «реверс» <] / (см. §110). (7) y = cp (x), где <p — обратное к φ, поэтому производная от x = φ (y) и ^ (y) равна <Y (y) и не равна нулю Если 9 (х) имеет производную 9 ‘(х) = гог
Фактически, если y (x — \ — h) = y ^ k, то 0-> 0 как — »- 0φ ‘(x) lim ((x + h) -9 (X) + _1 ) Людмила Фирмаль

