Оглавление:



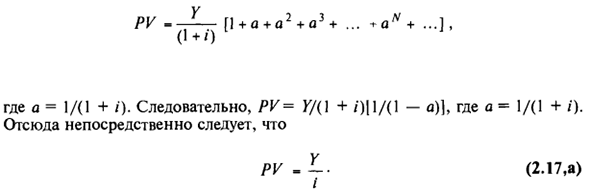

Некоторые динамические аспекты макроэкономики: ставка процента и приведенная стоимость
- Динамические аспекты макроэкономики: процентные ставки и текущая стоимость Многие важные макроэкономические вопросы связаны с решениями, которые принимаются не только в любой момент, но и включают время как фактор принятия решений. Решение семьи о сбережениях за определенный год фактически является решением, учитывающим временные факторы.
- Другими словами, стоит ли тратить деньги на потребление или позже. Сегодня спасающие домохозяйства лишают часть своего текущего потребления, чтобы расширить их охват в будущем. В этих случаях 5 Недавний набор на основе новых данных об иностранных инвестициях в США. Я свидетельствую. В 1990 году NUPb составил около 360 миллиардов долларов.
Т Блиц 2-10 Инвентарь против потока: некоторые примеры. Людмила Фирмаль
Тип связи: Инвентаризация увеличения потока акции Поток Капитал (С) финансы Богатство {W) Баланс иностранных инвестиций (L /// P) Государственный долг (O ») Чистые инвестиции (/ -DN) Сбережения (S) Текущий платежный баланс (CA) Дефицит бюджета (DEF) K- = J W- и / _1 = S NIIP-L /// P_1 = CA Dg-Dg_y = DEF
Мы считаем, что домохозяйства делают многопериодный динамический (с учетом временных факторов) выбор, то есть выбор, который касается распределения ресурсов в разное время. Решение компании о размере инвестиций в этом году также является динамичным с учетом временных факторов.
Фактически, компании должны решить, следует ли игнорировать текущие дивиденды или даже запрашивать дополнительные кредиты для расширения будущего производства и получения более высокой прибыли. В следующей главе мы рассмотрим лучшее долгосрочное многопериодное решение. Здесь нам необходимо ввести два важных элемента в анализ динамических решений: процентная ставка и чистая приведенная стоимость.
Процентные ставки — это просто основа, с помощью которой сегодняшние деньги и товары могут быть обменены на деньги и товары в какой-то момент в будущем. Например, предположим, что банковская ставка составляет 10% годовых. Это означает, что сегодняшний депозит составит $ 1,10 в следующем году, дополнительно $ 1.
Следовательно, можно сказать, что текущая стоимость 1 доллара в следующем году, то есть текущая стоимость этого доллара составляет 0,91 доллара. Вы можете использовать процентные ставки для расчета приведенной стоимости определенной суммы в будущем.
- Предположим, что процентная ставка составляет 10% в год, а текущая стоимость составляет 1 доллар США каждые два года. Как видите, текущая стоимость 1 доллара США в следующем году составляет 0,91 доллара, а продукт — 0,83 • 1,10 • 1J0, поэтому сегодняшний депозит в размере 0,83 доллара дает дополнительные 2 доллара в течение двух лет.
Поэтому, если вы сегодня внесете $ 1,74 (0,91 + 0,83), вы будете получать 1 доллар каждые 2 года. Короче говоря, текущая стоимость $ 1 в следующем году и $ 1 год спустя составляет $ 1,74. В более общем случае предположим, что процентная ставка в годовом исчислении /.
Далее рассчитайте текущую стоимость будущих доходов. Людмила Фирмаль
Да, обозначается буквой K и продолжается до года / Vth, например Y2 для первого года, Y2 для второго года, X3 для третьего года. Это соответствует доходу Y, требует Y {/ {1 + /). Точно так же, чтобы получить доход через 2 года, сегодня нам нужно Y2 / (1 + O2-.
Выполнение аналогичной операции для каждого года N дает текущую стоимость всей последовательности доходов из следующего уравнения: вы. PV ++ … (2.15) (1 + /) (1 + о2 (1 + О (1 + 0) Часто семье, компании или правительству необходимо решить, стоит ли инвестировать сегодня на сумму Y, равную 0/0, по причинам будущего дохода.
Чтобы понять рациональность инвестиционных решений, либо сравните приведенную стоимость последовательности доходов с суммой инвестиционных затрат, либо возьмите минус / ноль и прибавьте текущую стоимость будущего дохода к этой сумме, чтобы получить чистую приведенную стоимость инвестиций.
Вы можете рассчитать стоимость (NPV) и внести инвестиции: NPV в _ / + + … + * V. (2.16) (L + o (l + O2 d + o » Если NPV является положительным, инвестиционная идея принимается. Если отрицательный, предложение должно быть отклонено. (В следующих главах будут рассмотрены инвестиционные решения более подробно.)
Один конкретный очень важный случай связан с такими инвестициями, которые могут приносить одинаковую сумму дохода в единицу времени «навсегда». Например, рассмотрим облигацию, которая генерирует Y в году в любом году следующего периода (такая постоянная связь называется консолью). Текущее значение PV можно рассчитать следующим образом. PV + … + —… (2AT) (1 + 0 (1 + 02 (1 + 0 *)
Эта формула представляет собой сумму бесконечного числа слагаемых, а сумма представляет собой геометрическую последовательность, поэтому нетрудно найти ее значение. Из первичной алгебры известна следующая формула: 1 + a + a2 + a3 + … + aL ‘+ .. (1 день) Следовательно, соотношение (2.17) можно переписать следующим образом: Эта формула применяется только тогда, когда: /> 0 до K = K / (1 + /) |] / (1-a)], где a = 1 / (1 + /). Скоро продолжим (2.17, а) /
Смотрите также:
| Реальные и номинальные переменные | Роль ожиданий |
| Потоки и запасы в макроэкономике | Резюме |

