Натяжение

Натяжение

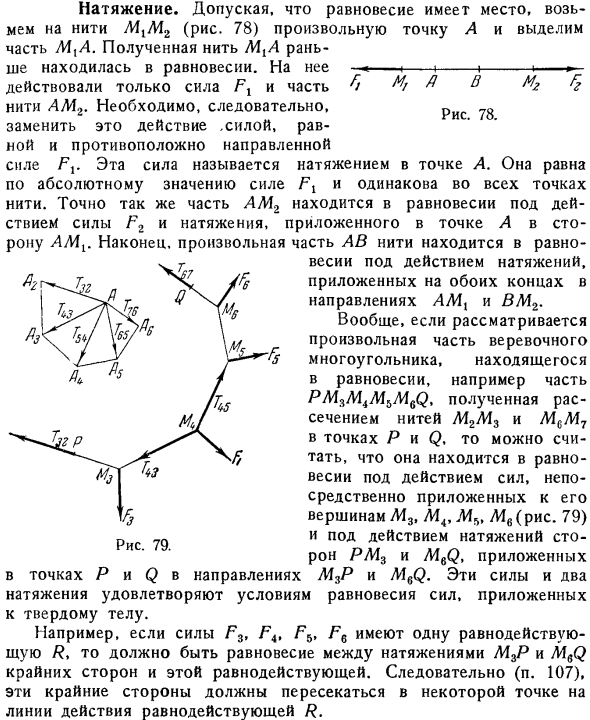
• Выберите любую точку A на потоке рис. 78, предполагая, что равновесие имеет место Часть МТА. Полученная цепочка MTA была ранее в равновесии. Действовала только сила нити AMg и часть 6. Поэтому необходимо заменить это действие равно противоположной по направлению силой. Сила Fj. Эта сила называется натяжением в точке А. сила Ft и абсолютные значения равны и одинаковы для всех точек нити.

Но тела, называемые твердыми, настолько мало деформируются, что этой деформацией в первом приближении можно пренебречь, если только приложенные силы не слишком велики. Людмила Фирмаль

Аналогично, часть АМ2 находится в равновесии под действием напряжения, приложенного к точке а в направлении сил F2 и AMt. Наконец, любая часть резьбы AB находится в равновесии под действием напряжения, приложенного к обоим концам направлений LL11 и BM2. В общем случае, рассматривая любую часть канатного многоугольника в сбалансированном состоянии, PM3M4 M5M6Q получают путем рассечения нити Помещено в часть примера L42L13 и L4sL47 в точках P и Q, можно предположить, что в равновесии под действием силы, приложенной непосредственно к вершинам и3,Л14,Л15, Мб рис. 79 и натяжение сторон ММ3 и M6Q, P и Q в сторону м3 P и Q mqq.

• Эти силы и 2 силы удовлетворяют условиям равновесия приложенной силы. В точке напряжения к твердому. Например, если силы F3, F4, F5, F6 имеют 1 равнодействующую силу, M. должно существовать равновесие между напряжением 3P и крайней стороной и этой равнодействующей force. As результат раздел 107, эти крайние аспекты должны пересекаться в какой то точке на линии действия R результата. Заменены одна другой без изменения механического состояния твердого тела. 99.

Найти положения равновесия точки М, помещенной на наружную поверхность эллипсоида, если М отталкивается неподвижной точкой Р с силой, пропорциональной расстоянию. Людмила Фирмаль

Тогда равнодействующая будет лежать на центральной оси. тетраэдра равнялась нулю. через четыре вершины. Для этого покажем, что суммы моментов относительно каждого из шести ребер тетраэдра равны нулю. Такое же абсолютное значение имеет и момент силы р. Примем плоскость, в которой лежат силы, за плоскость ху. равна нулю, то либо равнодействующая проходит через эти точки, либо имеет место равновесие. то возможно только равновесие. Более того, сумма их проекций на произвольную ось равна, очевидно, нулю. Переходим теперь к случаю произвольного многоугольника, проведенных из одной вершины, разобьем его на треугольники.

Смотрите также:

Решение задач по теоретической механике

Равновесие твердого тела. Упражнения	Равновесие веревочного многоугольника. Многоугольник Вариньона
Веревочный многоугольник	Условия на концах