Напряженное состояние при растяжении и сжатии
Для того чтобы иметь полное представление о прочности материала, необходимо знать действующие напряжения не только в плоскости поперечного сечения, но и по любому наклонному сечению.
Рассмотрим стержень, который находится под действием растягивающей силы 
(рис. 2.13). Как указывалось выше, в поперечных сечениях стержня, достаточно удаленных от точек приложения сосредоточенных сил, нормальные напряжения распределяются равномерно и определяются по формуле
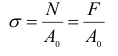
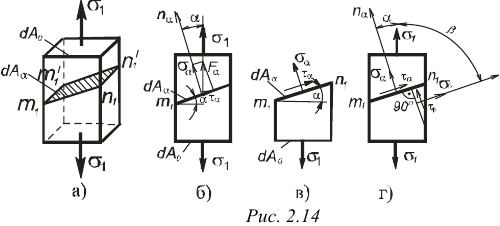
В окрестности какой-либо точки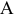 
, лежащей в плоскости поперечного сечения 
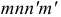(рис. 2.13), выделим бесконечно малый элемент (рис. 2.14, а). Поскольку по его граням, перпендикулярным направлению растягивающего усилия, действуют нормальные напряжения 
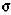, а остальные грани от напряжений свободны, то данный элемент находится в линейном напряженном состоянии (главное напряжение 
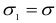, а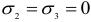 
). Условимся такой элемент изображать в виде плоской фигуры (рис. 2.14, б), хотя в действительности он имеет форму прямоугольного параллелепипеда.
Определим напряжения, возникающие в наклонном сечении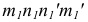 
(рис. 2.14, а), перпендикулярном к плоскости чертежа. Положение наклонной площадки определяется углом между направлением главного напряжения 
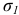и внешней нормалью 
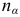к площадке (рис. 2.14, б). Этот угол принимают положительным, если его отсчитывают против часовой стрелки от направления 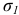. Наклонную площадку обозначают углом, определяющим ее положение. Так, для принятого на рис. 2.14, б обозначения угла имеем 
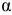-площадку.
По наклонной площадке вследствие однородности напряженного состояния для всех ее точек равномерно распределяются полные напряжения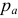 
, параллельные 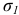. Составляющие полного напряжения, направленные по нормали к площадке и по касательной к ней, обозначим соответственно 
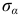и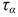 
. Для определения напряжени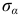й и 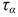применяем метод сечений. Так как наклонная площадка рассекла элемент на две части, отбросим одну из них (например, верхнюю) и рассмотрим равновесие оставшейся (нижней) части (рис. 2.14, б).
По направлению 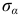действует, очевидно, нормальная сила 
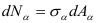, по направлению 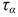— касательное усилие 
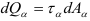и по направлению 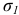— нормальная сила 
.
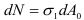Проектируя указанные силы на направления 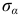и 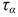соответственно получим
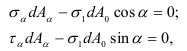
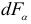— площадь наклонного сечения.
Учитывая, что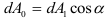 
, из уравнений равновесия имеем
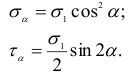
Воспользуемся формулами (2.12) и (2.13) для определения напряжений на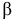 
-площадке, перпендикулярной к 
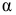-площадке (рис. 2.14, г). Нормаль 
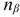образует с направлением 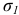угол
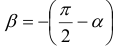
Заменив в формулах (2.12) и (2.13) угол 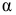на 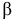, получим
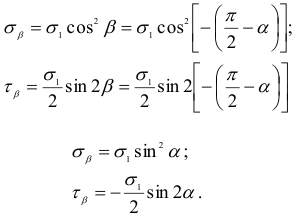
Для напряжени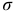й 
и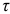 
, действующих по наклонным площадкам, принимаем следующее правило знаков: нормальное напряжение положительно, если оно растягивающее; касательное напряжение положительно, если для совпадения с его направлением внешнюю нормаль к площадке необходимо повернуть по часовой стрелке.
Отметим некоторые свойства линейного напряженного состояния, вытекающие из зависимостей (2.12) — (2.15).
- Сумма нормальных напряжений, действующих по двум взаимно перпендикулярным площадкам, постоянна и равна главному напряжению, т.е.
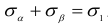. - На двух взаимно перпендикулярных площадках касательные напряжения равны, но противоположны по знаку, т. е.
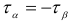. Данное свойство является общим для любого напряженного состояния и носит название закона парности касательных напряжений. - Величина нормального напряжения в любом наклонном сечении
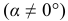меньше 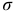, и достигнет максимума лишь в поперечных сечениях 
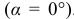. Касательное напряжение наибольшее значение имеет в сечении, составляющем угол 45° с направлением 
.
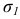В этом случае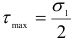 
.
Оценивая напряженное состояние стержня при его осевом растяжении или сжатии, можно сделать заключение о том, что стержень разрушается либо по поперечному сечению в результате действия максимальных нормальных напряжений, либо по наклонной (под углом 45°) плоскости от действия наибольшего касательного напряжения.
Эта теория взята со страницы лекций по предмету «прикладная механика»:
Возможно эти страницы вам будут полезны:
