Оглавление:




Напряжения в наклонных сечениях растянутых стержней
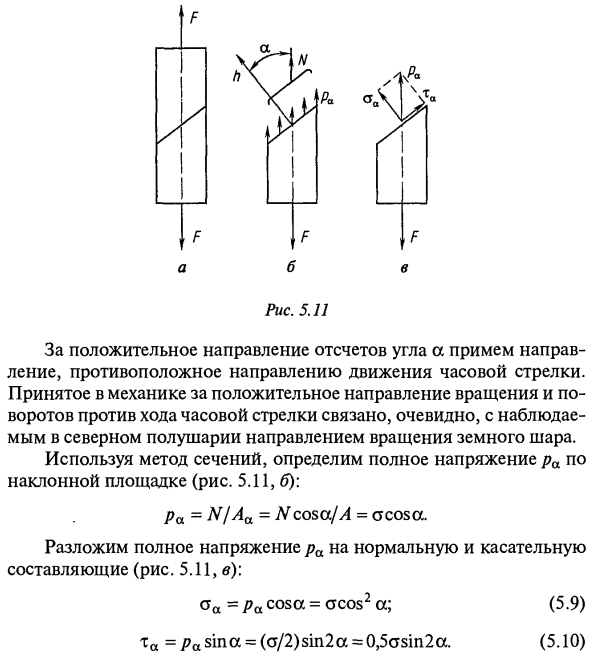
- Напряжение в наклонной части растянутого стержня Чтобы оценить прочность детали, рассмотрите напряжение, действующее на любой участок растянутого (сжатого) стержня. Нормальное напряжение сечения считается известным. Возьмите поперечное сечение, наклоненное под углом а к сечению (рис. 5.11, а). Наклонное поперечное сечение Aa = A / cosa.
Рисунок 5.11 В механике это считается положительным вращением и вращением против часовой стрелки, и оно явно связано с направлением вращения Земли, наблюдаемым в северном полушарии. Используйте метод поперечного сечения, чтобы определить общее напряжение ra на наклонной платформе (рис. 5.11, б): Pa = Нет / Aa = Ncosa / A = a cos a. Разложим общее напряжение pa на нормальную и тангенциальную составляющие (рис. 5.11, в): (5.9) (5.U) oa = pa cosa = acos ^ a; та = /? asina = (a / 2) sin2a = 0,5asin2a.
Для положительного направления показания угла a возьмите противоположное направление движения по часовой стрелке. Людмила Фирмаль
Изучите уравнения (5.9) и (5.10), чтобы определить нормальное и тангенциальное напряжение в зависимости от угла наклона площадки. В случае a = 0, т.е. в поперечном сечении, нормальное напряжение является максимальным, а касательная равна нулю. а = 90 °, т.е. в продольном разрезе нет нормального или сдвигового напряжения. Это означает, что продольные слои вытянутых стержней не имеют силового взаимодействия друг с другом вдоль боковых сторон, и удлинение стержня представляется как продолжение пучка параллельных прядей, которые не связаны друг с другом.
Максимальное касательное напряжение находится в поперечном сечении под углом 45 ° к поперечному направлению и равно половине напряжения поперечного сечения. Tmax = ^ a = 45 ° = 0,5a Оценивая напряжение в различных частях стержня при растяжении или сжатии, стержень в результате воздействия максимального нормального напряжения на поперечное сечение или в результате воздействия максимального тангенциального напряжения на поперечное сечение под углом 45 ° Вы можете видеть, что он разрушается.
Смотрите также:
| Определение механических свойств материалов Диаграмма напряжений | Закон парности касательных напряжений |
| Твердость материалов | Деформация сдвига |

