Напряжения в движущейся вязкой жидкости

Напряжения в движущейся вязкой жидкости

Напряжения в движущейся вязкой жидкости. Когда вязкая жидкость движется в нем, вязкая жидкость обладает способностью сопротивляться относительному движению ее слоев и частиц, в результате чего происходит не только перпендикулярное, но и сдвиговое движение stresses. To Обратите внимание, что нормальное напряжение может возникнуть только тогда, когда невязкая жидкость движется внутрь.

Если при движении жидкости преобладают силы вязкости, то характерным является ламинарный режим движения жидкости. Людмила Фирмаль

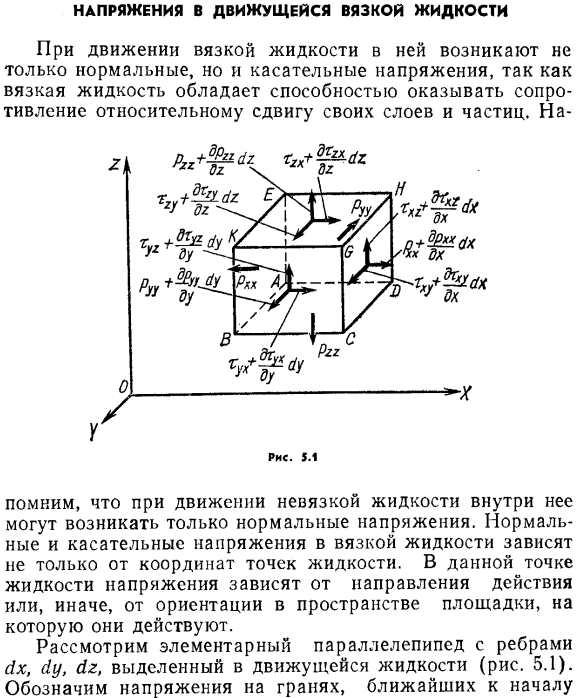
• Вертикальные и тангенциальные напряжения вязких жидкостей зависят не только от координат точек fluid. At в данной точке жидкости напряжение зависит от направления действия, или иначе, от направления пространства места действия. Рассмотрим основные параллелепипеда, который изолирован в движущейся жидкости с ребрами ХХ, уу, Ю. Г.(рисунок 5.1).

Указывает напряжение поверхности, ближайшей к начальной точке 89 координаты(авке, AENO, абсо), rxx в, посоветуйте, РЭГ, хх% хх, хх、 Гуг, деревья, деревья ’ Первый индекс указывает направление оси, на которой данная плоскость перпендикулярна, то есть направление нормали к плоскости, а второй индекс указывает направление напряжения, то есть к какой оси она параллельна.

• Таким образом, тангенциальное напряжение туфа действует на плоскость, перпендикулярную оси Op Amp и действует в направлении оси 0X \ xxx, перпендикулярном оси 02, и в направлении оси OX Предполагая, что напряжение непрерывно изменяется в объеме жидкости, получим значения напряжений для всех граней параллелепипеда, используя разложение функции напряжений ряда Тейлора(табл.5.1).

Обратите внимание на тангенциальные напряжения взаимно перпендикулярных участков, направленных вдоль нормали, в любой точке течения вязкой жидкости (без доказательств). Таблица 5.1 На краю. Обычный Касательная Авке. Усон. AE1YU вкас. Абсо. ЦЕНТР. Rxx. РХ-у ДХ ах Вот именно. Ух. , drgg, ПРГ-в ^ аг Хуо> этого ху + ху ДХ 77. −1 dhhg ХХ г \ ДХ Хох> ху Хоох + делать ДХ-г-2.

Если преобладают силы инерции, характерным является турбулентный режим движения потока. Людмила Фирмаль

• Hoogt делать грч> гормон роста ХХХ + ДТ? Икс дециграмм. 1 DX Ward ХГУ » Т ДГ Да. Да. <* У нацеливаюсь. нацеливаюсь. 90. Стресс. Линии пересечения этих участков равны между собой, то есть ghu = Ге> ХХХ тгз> хорошо-ГГУ Поэтому напряженное состояние вязких движущихся жидкостей характеризуется 6 независимыми компонентами напряжений.

Смотрите также:

Задачи по гидравлике

Возможно эти страницы вам будут полезны:

1. Уравнение Бернулли для частных случаев.
2. Энергетическая интерпретация уравнения Бернулли для установившегося движения.
3. Уравнения движения вязкой жидкости в напряжениях.
4. Соотношения между напряжениями и скоростями деформаций в движущейся вязкой жидкости.