Напряжения при изгибе. Расчеты на прочность
Как было показано выше, при изгибе величина нормальных напряжений зависит от величины изгибающего момента, а величина касательных напряжений — от величины поперечной силы. Изгибающий момент или поперечная сила в любом сечении балки могут быть определены рассмотренными выше методами, с помощью эпюр. При расчетах на прочность большое значение имеет распределение нормальных и касательных напряжений по сечению.
Установим зависимость между изгибающим моментом, действующим в сечении, и возникающими при этом нормальными напряжениями, а также определим закон распределения нормальных напряжений по сечению.
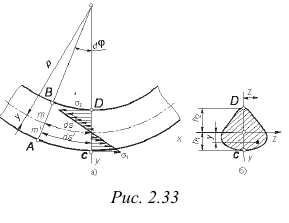
Пусть прямолинейная балка, имеющая продольную вертикальную плоскость симметрии, подвергается чистому изгибу под влиянием силовых факторов, действующих в этой плоскости (рис. 2.33). Указанную плоскость будем называть плоскостью изгиба. Выделим элемент балки, ограниченный двумя поперечными сечениями, находящимися на бесконечно малом расстоянии 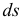 друг от друга. При изгибе ось балки (линия пересечения нейтрального слоя с плоскостью изгиба) искривляется, как показано штрихпунктиром на рис. 2.33, а, а сечения, ограничивающие выделенный элемент балки, поворачиваются вокруг нейтральных осей, проходящих через точки тип, и, заняв положения
друг от друга. При изгибе ось балки (линия пересечения нейтрального слоя с плоскостью изгиба) искривляется, как показано штрихпунктиром на рис. 2.33, а, а сечения, ограничивающие выделенный элемент балки, поворачиваются вокруг нейтральных осей, проходящих через точки тип, и, заняв положения  и
и  , образуют угол
, образуют угол 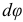 . При этом можно считать, что указанные сечения остаются плоскими, а расстояния между продольными слоями балки не меняются. Дуга
. При этом можно считать, что указанные сечения остаются плоскими, а расстояния между продольными слоями балки не меняются. Дуга 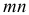 , принадлежащая нейтральному слою, сохраняет свою первоначальную длину
, принадлежащая нейтральному слою, сохраняет свою первоначальную длину 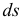 , а длина дуги
, а длина дуги 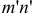 отстоящей на расстоянии у от нейтрального слоя, принимает новое значение
отстоящей на расстоянии у от нейтрального слоя, принимает новое значение 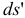 Радиус кривизны дуги
Радиус кривизны дуги 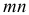 изогнутой оси балки можно считать постоянным. Обозначив его через
изогнутой оси балки можно считать постоянным. Обозначив его через 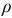 , имеем
, имеем
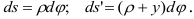
Относительное удлинение дуги
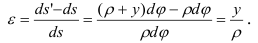
По закону Гука напряжение в слое, отстоящем на расстоянии 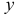 от нейтрального,
от нейтрального,
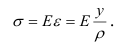
Таким образом, нормальные напряжения в поперечном сечении изогнутой балки прямо пропорциональны расстояниям от рассматриваемых точек до нейтральной оси (рис. 2.33, б), т. е. изменение напряжений по сечению в плоскости изгиба подчиняется линейному закону (рис. 2.33, а).
Из равенства (2.54) следует: 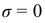 при
при 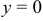 и
и 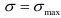 при
при 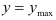 , т. е. нормальное напряжение равно нулю на нейтральной оси и достигает максимальных значений в наиболее удаленных от этой оси волокнах.
, т. е. нормальное напряжение равно нулю на нейтральной оси и достигает максимальных значений в наиболее удаленных от этой оси волокнах.
Рассматривая у как алгебраическую величину, имеющую положительное значение для растянутых и отрицательное для сжатых волокон, получим для напряжений в этих волокнах соответственно положительные и отрицательные значения.
На выделенный элемент  (рис. 2.33, а) действуют со стороны правой части балки распределенные по сечению
(рис. 2.33, а) действуют со стороны правой части балки распределенные по сечению  силы
силы
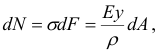
где 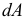 — элементарная площадка, расположенная на расстоянии
— элементарная площадка, расположенная на расстоянии 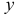 от нейтральной оси.
от нейтральной оси.
Эта система элементарных сил эквивалентна системе внешних сил, действующих на правую часть балки, сводящихся в данном случае к одному изгибающему моменту 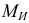 (поперечная сила
(поперечная сила 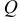 = О, так как мы рассматриваем чистый изгиб). Таким образом, главный вектор распределенных по сечению
= О, так как мы рассматриваем чистый изгиб). Таким образом, главный вектор распределенных по сечению 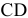 сил равен нулю, а главный момент их относительно любого центра равен изгибающему моменту в этом сечении. Поэтому при выбранной системе осей
сил равен нулю, а главный момент их относительно любого центра равен изгибающему моменту в этом сечении. Поэтому при выбранной системе осей
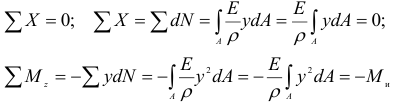
где 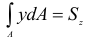 — статический момент площади сечения относительно нейтральной оси;
— статический момент площади сечения относительно нейтральной оси; 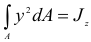 — момент инерции площади сечения относительно той же оси. Отсюда, так как
— момент инерции площади сечения относительно той же оси. Отсюда, так как
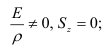
кроме того
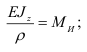
Из уравнения (2.55) следует, что нейтральная ось проходит через центр тяжести сечения, и она является одной из главных центральных осей инерции.
Уравнение (2.56) можно представить в виде
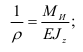
Величина 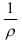 представляет собой кривизну изогнутой оси балки и характеризует величину деформации при изгибе. Произведение модуля упругости
представляет собой кривизну изогнутой оси балки и характеризует величину деформации при изгибе. Произведение модуля упругости 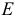 характеризующего механические свойства материала балки, на момент инерции сечения
характеризующего механические свойства материала балки, на момент инерции сечения 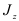 , характеризующий форму и размеры сечения, называют жесткостью при изгибе.
, характеризующий форму и размеры сечения, называют жесткостью при изгибе.
Из соотношения (2.57) следует, что величина деформации изогнутой оси балки прямо пропорциональна изгибающему моменту 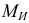 и обратно пропорциональна жесткости при изгибе
и обратно пропорциональна жесткости при изгибе 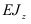 . Таким образом, жесткость при изгибе характеризует способность балки из данного материала с заданной формой и размерами поперечного сечения сопротивляться воздействию изгибающего момента.
. Таким образом, жесткость при изгибе характеризует способность балки из данного материала с заданной формой и размерами поперечного сечения сопротивляться воздействию изгибающего момента.
Подставляя в уравнение (2.54) выражение 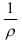 из уравнения (2.57), имеем
из уравнения (2.57), имеем
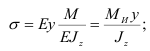
Наибольшие по абсолютной величине напряжения возникают на наиболее удаленных от нейтральной оси волокнах, т.е. при 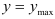 . Обозначим
. Обозначим
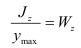
Величину 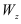 называют осевым моментом сопротивления сечения, т.е. момент сопротивления определяют как частное от деления момента инерции сечения относительно нейтральной оси на расстояние от этой оси до наиболее удаленной точки сечения.
называют осевым моментом сопротивления сечения, т.е. момент сопротивления определяют как частное от деления момента инерции сечения относительно нейтральной оси на расстояние от этой оси до наиболее удаленной точки сечения.
Условие прочности для балок, изготовленных из материала, одинаково сопротивляющегося растяжению и сжатию, имеет вид
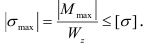
Балки из материалов, одинаково сопротивляющихся растяжению и сжатию, обычно изготовляют с сечениями, симметричными относительно нейтральной оси, т. е. 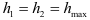 Для материалов, которые не обладают указанными свойствами, необходимо определять максимальные напряжения в крайних растянутых и сжатых волокнах. Полагая
Для материалов, которые не обладают указанными свойствами, необходимо определять максимальные напряжения в крайних растянутых и сжатых волокнах. Полагая 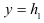 и
и 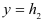 получим наибольшие по абсолютной величине напряжения в крайних точках сечения
получим наибольшие по абсолютной величине напряжения в крайних точках сечения  и
и 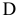 (рис. 2.33, б):
(рис. 2.33, б):
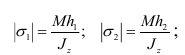
Обозначив допускаемые напряжения на растяжение и сжатие соответственно 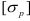 и
и 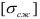 приходим к следующим уравнениям прочности при изгибе балок, для которых
приходим к следующим уравнениям прочности при изгибе балок, для которых 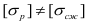 :
:
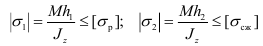
т. е. размеры и форма поперечных сечений изгибаемой балки должны быть подобраны так, чтобы абсолютные величины напряжений в крайних волокнах не превышали допускаемых напряжений на растяжение и сжатие.
Рассмотрим величины моментов сопротивления для наиболее распространенных форм сечения.
Для прямоугольника (см. рис. 2.32, с), с учетом соотношений (2.46) и (2.58′), при  осевой момент сопротивления
осевой момент сопротивления
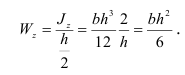
Для круга (см, рис. 2.32, б)
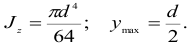
Осевой момент сопротивления
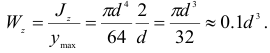
Для кольца (см. рис 2.32, в)
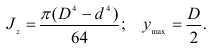
Осевой момент сопротивления
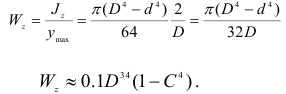
Для стандартных прокатных профилей моменты сопротивлений приведены в таблицах стандартных сортаментов.
Рассмотренный выше случай определения напряжений относился к чистому изгибу. Однако в общем случае поперечного изгиба наряду с нормальными в поперечных сечениях балки возникают касательные напряжения, связанные с наличием поперечной силы.
Определим приближенно величину касательных напряжений при поперечном изгибе. Двумя поперечными сечениями 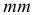 и
и 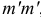 отстоящими на расстоянии
отстоящими на расстоянии 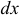 друг от друга (рис. 2.34, а), и продольной горизонтальной плоскостью
друг от друга (рис. 2.34, а), и продольной горизонтальной плоскостью 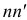 отстоящей на расстоянии у от нейтрального слоя, выделим часть балки
отстоящей на расстоянии у от нейтрального слоя, выделим часть балки 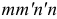 .
.
При поперечном изгибе на горизонтальной и вертикальных гранях выделенной части возникают потенциальные напряжения. В силу парности этих напряжений вместо напряжений в точках 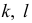 поперечного сечения (рис. 2.34, б) отстоящих на расстоянии у от нейтрального слоя, можно определить напряжения
поперечного сечения (рис. 2.34, б) отстоящих на расстоянии у от нейтрального слоя, можно определить напряжения 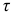 в соответствующем горизонтальном слое
в соответствующем горизонтальном слое 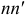 . Обозначим через
. Обозначим через 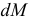 изменение изгибающего момента
изменение изгибающего момента 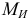 при переходе от сечения
при переходе от сечения 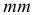 к сечению
к сечению 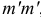 . При этом нормальное напряжение возрастает на величину
. При этом нормальное напряжение возрастает на величину 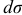 .
.
Полагая в качестве первого приближения, что касательные напряжения по ширине 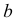 сечения распределены равномерно, и рассматривая равновесие выделенной части балки, имеем
сечения распределены равномерно, и рассматривая равновесие выделенной части балки, имеем
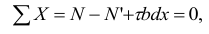
но
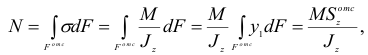
где 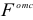 — отсеченная заштрихованная площадь:
— отсеченная заштрихованная площадь: 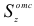 — статический момент этой площади относительно нейтральной оси
— статический момент этой площади относительно нейтральной оси 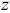 . Аналогично
. Аналогично
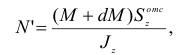
поэтому
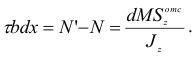
После преобразования с учетом выражения (2.33) получим формулу Журавского
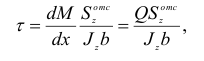
где 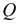 — поперечная сила в рассматриваемом сечении;
— поперечная сила в рассматриваемом сечении; 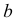 — ширина сечения;
— ширина сечения; 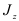 — момент инерции сечения относительно нейтральной оси;
— момент инерции сечения относительно нейтральной оси; 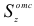 — статический момент площади отсеченной части сечения относительно нейтральной оси
— статический момент площади отсеченной части сечения относительно нейтральной оси 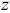 .
.
Так, для случая, показанного на рис. 2.35, а, статический момент отсеченной заштрихованной части определяется из соотношения
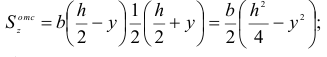
это уравнение параболы.
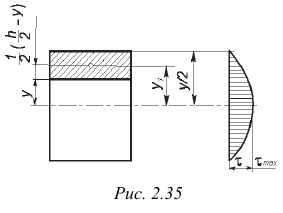
Касательное напряжение с учетом выражений (2.62) и (2.44)
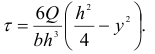
На рис. 2.35, б показана эпюра касательных напряжений, построенная по трем точкам:
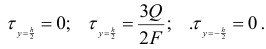
Для балки прямоугольного сечения касательное напряжение достигает максимального значения на уровне нейтральной оси:
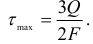
В общем случае максимальное касательное напряжение
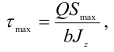
где 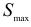 — статический момент всей части сечения, расположенный по одну из сторон от нейтральной оси.
— статический момент всей части сечения, расположенный по одну из сторон от нейтральной оси.
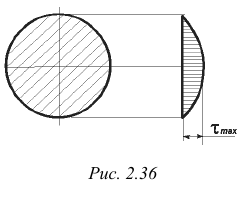
С известным приближением формула Журавского может быть применена и для таких сечений, как круг или кольцо. Эпюра касательных напряжений для круга показана на рис. 2.36. Здесь, так же как и в рассмотренном случае в наиболее удаленных от нейтральной оси точках сечения, касательное напряжение равно нулю и достигает максимума на нейтральной оси, причем для круга 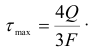 , для кольца
, для кольца 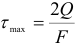 . Касательная напряжения равны нулю и в наиболее удаленных от нейтральной оси точках таких сечений, как двутавровое, крестообразное и
. Касательная напряжения равны нулю и в наиболее удаленных от нейтральной оси точках таких сечений, как двутавровое, крестообразное и  -образное.
-образное.
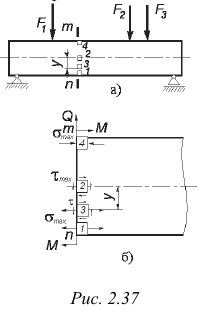
В общем случае поперечного изгиба условие прочности зависит от напряженного состояния в опасной точке. Рассмотрим характер напряженного состояния четырех точек сечения 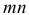 балки, изображенной на рис. 2.37, а, б. Анализ показывает, что: а) элементы 1, 4, расположенные на крайних волокнах, имеют касательное напряжение
балки, изображенной на рис. 2.37, а, б. Анализ показывает, что: а) элементы 1, 4, расположенные на крайних волокнах, имеют касательное напряжение 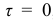 , нормальное напряжение
, нормальное напряжение 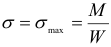 ; таким образом, налицо линейное напряженное состояние;
; таким образом, налицо линейное напряженное состояние;
б) элемент 3, расположенный на расстоянии 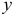 от нейтрального слоя, имеет на вертикальных гранях
от нейтрального слоя, имеет на вертикальных гранях 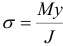 и
и 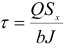 на горизонтальных гранях касательные напряжения
на горизонтальных гранях касательные напряжения 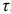 ; элемент находится в плоском напряженном состоянии;
; элемент находится в плоском напряженном состоянии;
в) элемент 2 на нейтральном слое не испытывает действия нормальных напряжений 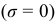 ; касательные напряжения на вертикальных и горизонтальных гранях достигают максимального значения
; касательные напряжения на вертикальных и горизонтальных гранях достигают максимального значения 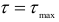 .
.
Длительная практика эксплуатации изогнутых балок показывает, что наиболее опасной, определяющей работоспособность конструкции, является точка, расположенная на крайних растянутых волокнах (элемент 1).
Следовательно, основным уравнением, по которому проверяют прочность или определяют размеры сечения, является
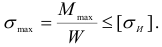
В некоторых специфических случаях, когда касательное напряжение может оказаться решающим фактором, определяющим прочность изогнутой балки, производят полный расчет балки по эквивалентным напряжениям, определенным с помощью одной из теорий прочности.
Эта теория взята со страницы лекций по предмету «прикладная механика»:
Возможно эти страницы вам будут полезны:
| Поперечная сила и изгибающий момент |
| Геометрические характеристики плоских сечений |
| Кручение стержня круглого поперечного сечения |
| Чистый сдвиг и его особенности |

