Оглавление:




Напряжения и деформации при растяжении и сжатии
- Напряжение и напряжение И сжатие Сначала рассмотрим простейший случай удлинения призмы с равномерно распределенными на обоих концах продольными нагрузками (рис. 21, а). Площадь поперечного сечения F. Внешняя нагрузка, создаваемая на каждом конце стержня, равна P и приложена к центру тяжести
конца. Нормальная сила m-n любого сечения (рис. 21, б) N = P Сила N — это результирующая сила внутренней силы cdF, действующей на микрозону JV = J adF на поперечном сечении стержня. F Однако из уравнения (2.2) невозможно найти закон нормального
напряжения a по сечению. Другими словами, одного уравнения равновесия Людмила Фирмаль
недостаточно. Эксперименты показывают, что когда система взаимно перпендикулярных линий применяется к рассматриваемой поверхности древесины (рис. 21, а), горизонтальные линии aa, bb, cc перемещаются параллельно после загрузки стержня. Было Это означает, что все продольные волокна стержня вытянуты одинаково. «Естественно предположить, что внутренние продольные волокна равны, то есть они простираются в поперечном направлении. (2.2)
Указывает, что поперечное сечение смещено параллельно исходному положению, соответствующему первому и второму разрезам, представленным первым голландским ученым Д. Бернулли. Согласно этой гипотезе, участок, который был плоским до деформации, остается плоским после деформации. Гипотеза Бернулли широко используется в проблеме материального сопротивления. Поскольку все продольные волокна стержня находятся в одинаковом состоянии, нормальное напряжение во всех точках поперечного сечения должно
- быть одинаковым. a-const, следовательно, из уравнения (2.2) N = oF, ° = (2.3) Все приведенные выше соображения и уравнение (2.3) также применимы к сжатым коротким стержням *. б ААББ // 22 Рисунок 22 А Я 1 Я 1 Я 1 1 1 1 1 1 G 1 1 1 1 | 1 Я 1 дз + тидз ! , B ———————— б Рассмотрим напряжение, возникающее в результате растяжения и сжатия призмы. При растяжении длина стержня увеличивается, а поперечный размер уменьшается. И наоборот, сжатие уменьшает длину стержня и увеличивает боковые размеры. На фиг.22 пунктирной линией показана фигура деформации | вытянутого | растянутого стержня. Изменение начальной длины стержня A /
называется абсолютным удлинением и измеряется в единицах длины. Разрежьте мысленно бесконечно малый элемент стержня длиной dx. После применения нагрузки он получает расширение ЛСД. Продольная линейная деформация этого элемента (см. § 5) e =; Adx = zdx. ▼ * Если вы сожмете длинный стержень, он может набухнуть в сторону. Это явление понято гл. Xv. 24 суммируя удлинение мелких элементов по всей длине стержня с учетом простых напряжений a = const и s = const всех сечений, Следовательно, продольная деформация с простым ростом (2.4) Точно так же. Существует боковое искажение в направлении измерения а (рисунок 22): Я £ = но но (2.5)
Направление размера b h = -b Здесь ставится знак минус, потому что боковое Людмила Фирмаль
измерение уменьшается из-за растяжения. Для изотропных материалов боковое напряжение одинаково: Я Штаммы е и е ‘являются безразмерными величинами. Отношение поперечной деформации к продольной деформации, взятой при абсолютной величине простого растяжения или сжатия, называется коэффициентом Пуассона. H = (2.6} | £ | Коэффициент Пуассона (безразмерное количество) был назван в честь французского ученого впервые в начале 19 века. Человек, который обращает внимание на постоянство этих отношений. Пуассон сделал этот коэффициент равным 0,25, одинаковым для всех материалов. Дальнейшие эксперименты показали, что коэффициент Пуассона постоянен
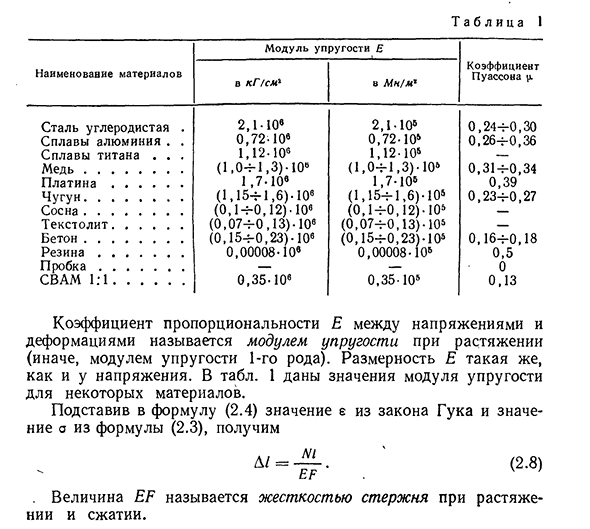
только для определенных материалов в пределах упругой деформации. Для различных материалов коэффициент Пуассона находится в пределах 0y. 0,5. В таблице. В таблице 1 приведены значения коэффициента Пуассона для нескольких материалов. Существует связь между стрессом и напряжением, известная как закон Крюка *. Форма центрального напряжения (сжатия) а = она (2.7) ▼ * Пожалуйста, обратитесь к §1. 25T a b l i c a 1 Название материала Модуль упругости E 1 Коэффициент Пуассона р. кг / см2 в Мн / м2 Углеродистая сталь 2.1.10e2.1.10®0.244-0.30 алюминиевый сплав. , 0.72.10e0.72-10®0.264-0.36 титановый сплав. , , 1.12.10e1.12-10®-Med ……… (1,04-1,3). 10e (1,04-1,3) -10®0,314-0,34 Платина
………………………………… 1,7,10e1,7-10®0, 39 часов. , , , , , , (1,154-1,6) -Y6 (1,154-1,6) -10®0,234-0,27 сосна ………………….. , (0,14-0,12) -10e (0,14-0,12) -10®-техксолит ………………. (0,074-0, 13 ). 10е (0,074-0,13). 10®-бетон ……….. (0,154-0,23) .10е (0,154-0,23) -10®0,164 -0.18 Резина … 0.00008-10e0.00008-10®0.5 P ab ……….. ……….— 0 SWAM 1: 1 ………………. 0.35.10 e0.35-10®0.13 Коэффициент пропорциональности между напряжениями E Напряжение и деформация называются модулем растяжения (или модулем типа 1). Размер E соответствует напряжению. В таблице. На рисунке 1 показан модуль упругости нескольких материалов. Подставляя значение e из закона Гука и значение a из уравнения (2.3) в уравнение (2.4), Д / = -. (2.8) EF. , Значение EF называется жесткостью стержня при растяжении и сжатии.
Смотрите также:

