Оглавление:






Напряжения и деформации при кручении стержня с круглым поперечным сечением
- Напряжение и напряжение кручения Круглый поперечный срез Положим сетку, образованную системой вертикальных линий, на сторону витой штанги (окружности), составляющую внешний контур сечения (формы) (рис. 168). После скручивания, после того, как прямоугольник, образованный сеткой, искажен, ось стержня остается прямой, а профиль деформированного участка (круглый и плоский до
деформации) остается тем же, в то время как скручивание находится под одним углом относительно другого. Когда происходит вращение сечения, это называется углом Поскольку расстояние между 187 изогнутыми участками существенно не изменяется, это означает, что продольные волокна не становятся длиннее или короче. Описанные наблюдения характеризуют деформацию волокон на поверхности стержня, но нельзя сделать
никаких выводов относительно деформации внутренних волокон. Чтобы прояснить этот вопрос, мы Людмила Фирмаль
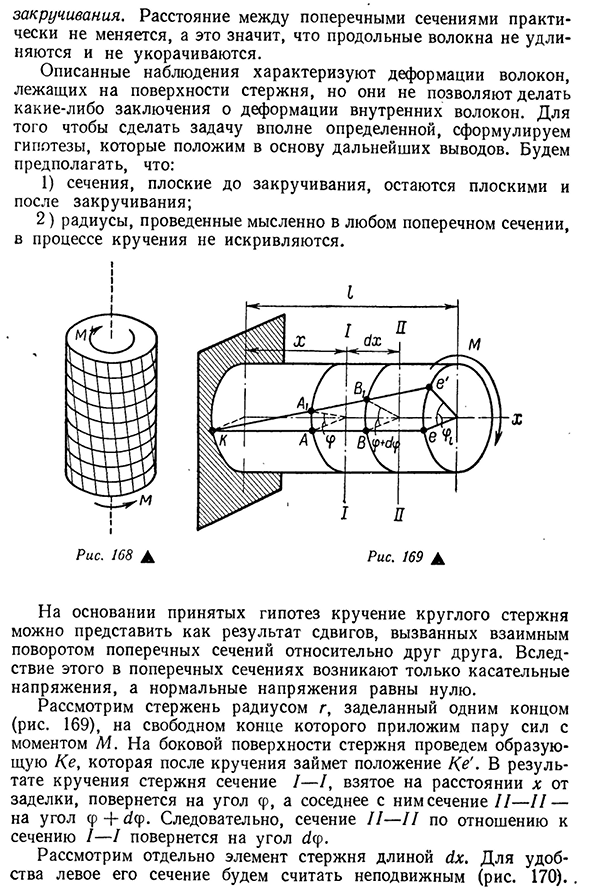
выдвигаем гипотезы, которые составляют основу для дальнейших выводов. Мы предполагаем, что: 1) сечение, плоское до скручивания, остается плоским после скручивания, 2) в процессе скручивания радиус, нарисованный мысленно в любом сечении, равен Я Я Я Я Я Я Рис 168А Исходя из принятой гипотезы, скручивание круглых стержней может быть выражено в результате сдвига, вызванного взаимным вращением поперечных сечений относительно друг друга. В результате в поперечном сечении создается только тангенциальное
напряжение, а нормальное напряжение равно нулю. Рассмотрим стержень радиуса g, уплотненный с одного конца (рис. 169), на свободный конец которого мы прикладываем момент М и пару сил. Нарисуйте пласт Ke, займите положение Ke после его закручивания ». Сечение / -I взято на расстоянии x от уплотнения в результате закручивания стержня, вращающегося на угол AB dx Для любого волокна, отстоящего от центра вала на расстояние p, имеем Tr = CCj_p
- dtp DC-dx (см. §38), две указанные точки могут быть записаны на основе закона Гука при переключении: (7.5) Сравнивая уравнения (7.4) и (7.5), мы видим, что касательное напряжение в точках поперечного сечения изменяется пропорционально расстоянию между этими точками от оси. Самое высокое напряжение Они находятся в самой дальней точке от центра шахты. Поэтому мы рассмотрели закон изменения t в радиусе поперечного сечения круговой оси. Графически этот закон показан на рисунке. 171, а) Для оси кольца закон распределения касательных напряжений показан на рисунке. 171,6 Значения, включенные в уравнения (7.4) и (7.5),
могут быть получены из условия, что действует тангенциальное напряжение 189 дана пара, равная крутящему моменту М согласно поперечному сечению вала. 171 а). Момент этой силы на оси стержня dMx = Tr dFp. Суммируя основные моменты, находим суммарный крутящий момент: (7.6) Подстановка значения Tr из (7.5) вместо формулы (7.6) дает следующее: F J «ZG d F P- Обратите внимание, что из точек сечения они одинаковы, и выражение P2dF = J p представляет между полярными моментами F Инерционный раздел. После этого или GJp dx ‘
Присвойте найденное значение формуле (7.5) (А) Аспирантура Получить относительно В этой формуле t может быть Людмила Фирмаль
определено в любой точке круглого сечения. Максимальное напряжение на поперечном полюсе составляет 1 Значение 1gr = __L называется моментом полярного сопротивления круглого сечения. Как уже упоминалось в главе VI, полярный момент инерции для непрерывного кругового сечения 190 для кольцевого сечения наружного диаметра D и внутреннего диаметра d куда d а = -. D Следовательно, момент сопротивления имеет следующее значение: W. = nd3unit описание в списках = д / 2 16 ‘ Для круглого сечения — F = Д / 2 = шестнадцать (1-4). Уравнение (а) используется для определения угла закручивания. D.MX dx f = -G J- После интеграции мы получим
полный угол закручивания стержня. % = f dx. (7.8) Когда f (Момент не изменяется по всей длине стержня, вал имеет постоянный диаметр, а интегрирующее уравнение (7.8) дает b = (7.9)) Значение GJP называется жесткостью при кручении стержня. Характеризует устойчивость вала к вращению. Для ступенчатых стержней для стержней, где M x неожиданно изменяется на длину, угол закручивания между первым и последним участком вала рассчитывается как сумма MH Задать угол закручивания секции — • Mxi-Qj-. (7,10) Идеальный угол поворота 191 всегда может
характеризовать жесткость на кручение стержня. Поскольку длина крутящего момента стержня может иметь разные знаки, общий угол кручения, найденный по уравнению (7.10), может быть небольшим, но в некоторых областях, для оценки жесткости стержня, другой Средство введено-угол поворота (7,11) 1 1 Имея размеры —- I I I —— г г см м Если график M x постоянен на разных участках сердечника, значение 6 численно равно углу поворота вала на единицу длины.
Смотрите также:
| Вычисление моментов инерции сложных фигур | Действие ударных и импульсивных нагрузок на упругие системы |
| Вычисление крутящих моментов и построение их эпюр | Постановка вопроса о прочности |

