Оглавление:




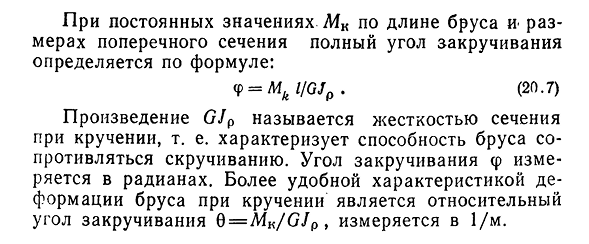

Напряжения и деформации при кручении бруса круглого поперечного сечения
- Характер распределения деформации при кручении круглого поперечного сечения балки составляет 20.2, которая нанесена на ее поверхность в виде параллельного круга и прямоугольника, состоящего из продольных линий, параллельных оси продольного направления стержня. Под действием мск прямоугольного момента кручения на поверхности балки продольная линия при наклоне
смещается, внешний вид окружности не изменяется, их взаимное расстояние приблизительно равно 20,2, б). В твисте есть еще n^один поворот сечения на несколько углов-угол закрутки, расстояние между параллельными окружностями не меняется. Предположим, что характер деформации, наблюдаемый на поверхности, одинаков
и внутри балки, что эквивалентно введению следующей гипотезы: 1) Людмила Фирмаль
поперечное сечение является плоским до деформации 1. таким образом, деформация при кручении балки круглого поперечного сечения возникает в результате вращения поперечного сечения, где только напряжение Рассмотрим стержень круглого сечения с жесткой прижимной опорой сечения B и сечения C внешним крутящим моментом l4sc (нагрузка 20.3, a). Выберем бесконечно малый элемент длины dz из бруска расстояния z двумя смежными участками,
перпендикулярными его оси. Понятно, что взаимный угол поворота двух соседних участков элемента dz будет равен t / F. 204 стр. 20.2 Кроме того, при малом угле y положение DK(рис. 20.3, 6). Угол сдвига y из-за малости этого угла равен tg y » y=KK-JDK=KK-Jdz. С другой стороны, tgd(p » d(p=7<<<<] / r, откуда KK=*=rdy, следовательно y-rdq/dz. (20.1) для внутренних волокон, расположенных на расстоянии р от центра тяжести сечения, угол сдвига мфжно записать в таком виде: yp=pd(p/dz. (20.2) Используйте правило сдвига крюка, чтобы найти касательное напряжение в интересующей точке.t=yQ=: Grdq / dz(20.3)
- Tr=7P G=Gpdy/dz. (20.4) Таким образом, в поперечном сечении балки при кручении возникает тангенциальное напряжение t, направленное в каждую точку перпендикулярно радиусу. Величина напряжения сдвига пропорциональна расстоянию каждой точки от центра поперечного сечения. В центре тангенциальные напряжения равны нулю, в точке, расположенной в непосредственной близости от внешней поверхности балки, они достигают наибольшего значения. График тангенциального напряжения вдоль произвольного радиуса представлен наклонной линией(рис. 20.3, б). Найдена зависимость
между моментом l1k, действующим на поперечное сечение балки, и касательным напряжением. Рассмотрим произвольную область dA, расположенную в плоскости поперечного сечения и на произвольном расстоянии p от центра поперечного сечения. 20.3, 6). Там крутящий момент. 205 страница 20.3 Рис 20,4 Полученное тангенциальное напряжение действует на все точки сечения, и тогда можно записать: к м=.1тр КПК. Присвоив интегральное значение=pGdy/dz, получим Mk={G (dyldz) p? Да Но Поскольку Gdcp/dz=const,$p2dA=JQ.
Момент инерции сечения, в итоге получаем MK=GJp dy/dz, Откуда он взялся Ди!dz=Mk / GJp. (20.5) полученное значение dqjdz подставляется в Людмила Фирмаль
Формулу (20.4) для нахождения касательного напряжения в любой точке поперечного сечения балки, представленного MK и / P : (20.6) 206 максимальное касательное напряжение (при p=g), возникающее вблизи внешней поверхности балки), Где Wp — полярный момент сопротивления поперечного сечения балки: W p^J p1G. : Сопротивление момента полярности секции — это отношение инерции момента полярности к расстоянию от центроида секции до самой дальней точки. Указанный момент полярности сопротивления равен м3 или см3. Для круглого сечения Jp=n G4 / 2 сопротивление полярного момента lF p=Jp/g=l g3 / 2. Аналогично вычисляется
напряжение сдвига на кручение стержня, имеющего круглое сечение, так как свойства деформации круглого сечения совпадают. Касательное напряжение направлено перпендикулярно радиусу во всех точках поперечного сечения, а участок t вдоль поперечного сечения представлен наклонной линией(рис. 20.4). Тангенциальное напряжение на внутренней поверхности кольца определяется по формуле: S b=^^p-величина тангенциального напряжения на внешней поверхности кольца (здесь оно достигает наибольшего значения) определяется по формуле: TSH.X=L * * rlJp=M^> Здесь Wp-полярный момент кольцевой части. Для кольцевого сечения момент
Полярной инерции равен J1=n(r4-G4)/2, тогда время полярного сопротивления кольца Вт к п =l (G6-L4)/2G. Из Формулы (20.5) находим взаимный угол поворота двух соседних сечений для элементов длины dz: d y=(Mk/GJp) d z. Для стержня длины I суммарный угол кручения равен сумме взаимных углов поворота его элементов dz. F=/(Mk / GJp) dz. Постоянная величина длины 207-стержневого АФК и-размер поперечного сечения идеального угла скручивания определяется по формуле: Ф=(20.7) Произведение G/p называется жесткостью сечения при кручении. Угол Ф поворота измеряется в радианах. Более удобной особенностью деформации балки при кручении является 1/м. относительный угол кручения измеряется при Q=ME / GJP.
Смотрите также:
Решение задач по технической механике
| Вычисление моментов инерции сложных сечений | Расчет на прочность и жесткость при кручении |
| Крутящие моменты. Построение эпюры крутящих моментов | Изгиб прямого бруса. Основные понятия |

