Оглавление:







Направление вогнутости кривой
- Направление кривизны Н°1.Вогнутый direction. In некоторые вопросы по теории сопротивления материала, понятие направления кривой вмятины*играет определенную роль. Представьте себе прямую K с уравнением y = f(x)>с определенным касательным Mt в точке M (x * y0).Если все точки линии, достаточно близкие к точке M, находятся
обращена (или ориентирована) вогнутой вверх (и выпуклой вниз).Напротив(рис. 177), если точка кривой, достаточно близкая к Mt, находится ниже касательной Mt, то кривая точки M называется выпуклой внизу (выпуклой вверху). Замечание. Читатель обращает
на касательной ( * ) Mt (рис. 176), то они говорят: Кривая точки M Людмила Фирмаль
внимание на то, что его интересует только точка кривой К, которая находится вблизи точки соприкосновения М. точка удалена от м.、 Например, кривая, показанная на диаграмме, имеет вид interest. In рис. 176, точка А этой кривой находится ниже касательной
линии ML, но она направлена вверх в точке M. 177. Возникает вопрос об аналитической функции, с ее помощью можно определить, в каком направлении изгибается кривая по вогнутой поверхности. Предположим, что во всех точках M (x, y) кривой кривая повернута вверх вогнутой поверхностью. Затем кривая будет показана, как
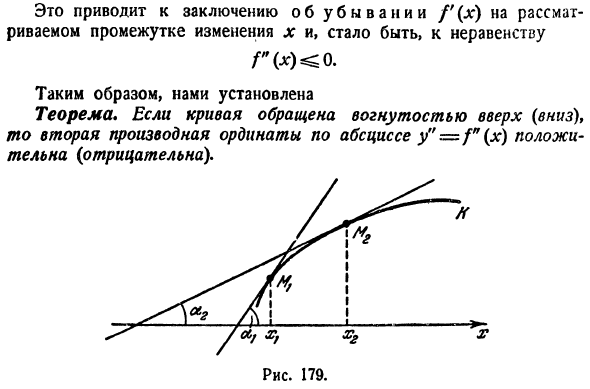
- показано на рисунке. 178.Возьмем 2 точки кривой Mx (X X y \ M%(x y% \x y%), где мы рисуем касательную к кривой. пусть aj и < η-углы, под которыми эти касательные образуют оси Ox. Вы можете увидеть его прямо с рисунка. Что?! Рисунок 178. Однако, tg a, tg» * П*> > ПхЬ Это приводит к выводу, что f ’(x) уменьшается в рассматриваемом
интервале вариации x, и поэтому становится неравенством. Р С *)<0. Поэтому, мы устанавливали 2-я производная ординаты относительно абсциссы Y = f (x) положительна (<отрицательна), если кривая теоремы повернута вверх (вниз) вогнутой поверхностью. Эта теорема обратима. То есть, зная знак 2-й производной, можно ответить
на вопрос, где находится вогнутая поверхность кривой directed. In факт, например f ’(x)> 0 Людмила Фирмаль
, первая производная f’(x) увеличивается с x. это означает, что при увеличении абсциссы x угол, образованный касательной кривой, проведенной по оси Ox и точке M (x, y), также увеличивается. То есть, если вы двигаетесь слева направо вдоль кривой, наклон кривой увеличивается. Но те же
фотографии. 178 указывает, что кривая вогнута и направлена вверх. Все вышеперечисленное можно суммировать с помощью планшета. Кривая вогнутого направления со знаком G (x) Верхний+ Вниз- н°2.Точки перегиба и коррекции points. Do не думайте, что вся кривая всегда вогнута в одном и том же направлении. Обычно ситуация несколько сложнее: интервал изменения абсциссы х делится
на части, на которых кривая попеременно поворачивается вогнутой вверх и вниз. Точка M кривой, которая разделяет участки, отличающиеся в направлении вогнутости кривой определения, является、 Точка перегиба кривой. Точка перегиба — это не только точка Af, которая находится на кривой, но также называется
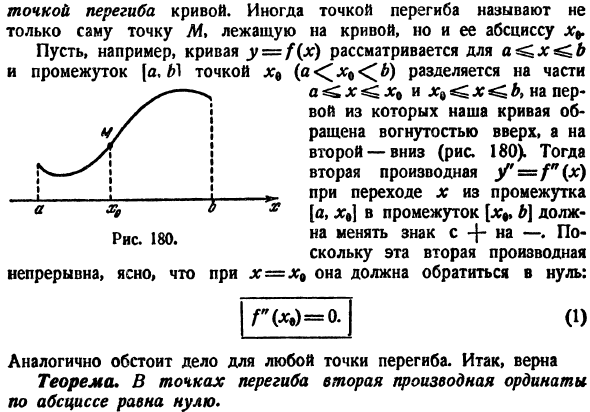
ее абсциссой. Например, предположим, что кривая y = f (x) является a ^ x ^ b, а интервал[a, b \разделен точкой (a <^ x0 <^ b). x ^^ x ^ b. первая кривая изгибается вогнутой поверхностью вверх, а вторая-вниз(рис.180).Тогда 2-я производная V = f (g), когда x достигает интервала[X * b \из интервала[a, x9\, требуется для jgQ путем
изменения знака from-f—.By Поскольку эта производная 2-го порядка непрерывна, если x = x9, она должна исчезнуть. Да.) ГМ = о. Что касается точки перегиба, то ситуация аналогичная. О, да. Теорема в точке перегиба 2-я производная ординаты по отношению к абсциссе равна нулю. Однако эта теорема необратима. Из того факта, что отношение(1) заполнено некоторой точкой x0, нет абсолютно
никакого способа для x% быть точкой перегиба. Например, рассмотрим кривую y = dL. Здесь Y = 12. * ?Это isSo, во всех x, кроме* = 0, где y = 0, Y> 0.So кривая не имеет точки перегиба при x = 0 по всей своей длине, но для этого x она будет Y = 0.Тем не менее, кривая y =
f(где X \ ’ S (1) имеет место) является чисто геометрически важной. (Xo, yo) (и его абсцисса x0) ((1) удерживается) называется прямой точкой кривой y = f (x) (происхождение этого выражения раскрывается читателю после прочтения§ 4).На пути все точки перегиба являются его выпрямлением, но не наоборот. Исследование вогнутости кривой аналогично исследованию функции экстремума, но вместо знака
первой производной f ’(x) следует обратить внимание на знак второй производной f «{x)*. Rules. To выясним свойства вогнутой поверхности кривой y = f (x\, нам нужно: 1) Найти гамму (x \ 2) / » (jc)= 0 для решения этого уравнения. Его корни Представляет точку, в которой кривая выпрямляется. 3)точка X \% X на числовой оси * …нарисуйте
xm и определите anaki f «(x)в результирующем сечении оси. Образцы. Изучите вогнутую кривую у = Х *-14х * + 60jc * −9. Решение. Последовательно найти Y = 4 * * — 42l * + 120zh + 8, y «= 12l; » — 84 * + 120. Если я положу Y = 0 и уменьшу его до 12, я получу уравнение йк *-7х + * 10 = О Корни= 2,= b. оси делятся на отрезки (—oo, 2), (2, b), (b,+ oo). чтобы установить знак y в этих отрезках, мы утверждаем следующее: Если абсолютное значение x очень велико, то Jt * значительно
превышает x. So существуют разделы(-oo, 2) и (5,+ oo) Y> 0*).Я тебе верю. Вы можете видеть, что Y (3)=-24, и оттуда (2, 5) будет Y <0.So кривая будет вогнутой вверх при x <^ 2 и вогнутой вниз при 2 <^ <[5.Мы видим, что точка x = 2, x = b является точкой перегиба.
Смотрите также:
| Формула Тейлора | Параметрическое задание кривой |
| Касательная и нормаль | Кривизна |

