Оглавление:
Задача №1.2.8.
Наклонная плоскость, образующая с горизонтом угол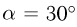 
, движется с ускорением а, направленным влево, как показано
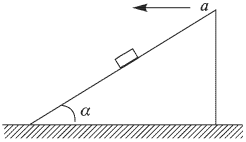
на рисунке. При каких значениях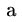 
тело, находящееся на наклонной плоскости, будет скользить вверх вдоль нее? Коэффициент трения между телом и плоскостью 
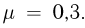Ускорение свободного падения принять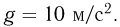 
Решение:
Рассмотрим случай, когда ускорение наклонной плоскости таково, что тело не скользит по ней. Тогда в неподвижной системе
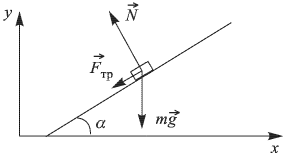
отсчета сумма сил, действующих на тело (см. рисунок), сообщает ему ускорение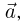 
направленное горизонтально. Если при этом сила трения покоя достигла своего максимального значения 
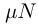, то в проекциях на ос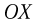и 
и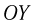 
неподвижной системы уравнение движения тела имеет вид:
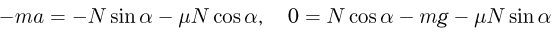
Из второго уравнения находим величину нормальной составляющей силы реакции наклонной плоскости:
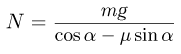
После подстановки этого выражения в первое уравнение, после несложных преобразований определяем значение ускорения, при котором выполняются перечисленные выше предположения:
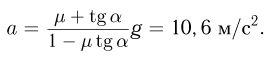
Если ускорение наклонной плоскости превышает найденное значение на любую сколь угодно малую величину, тело начнет скользить вверх, поскольку сила трения уже не сможет его удерживать. Если же коэффициент трения таков, что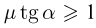 
, тело не будет скользить вверх при любых ускорениях.
Эти задачи взяты со страницы решения задач по физической механике:
Решение задач по физической механике
Возможно эти задачи вам будут полезны:
