Задача 3.13.
Найти точки экстремума функции
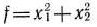
при условии
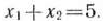
Решение:
Составим функцию Лагранжа
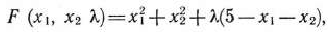
найдем ее частные производные по 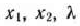 приравняем их нулю. В результате получим систему уравнений
приравняем их нулю. В результате получим систему уравнений
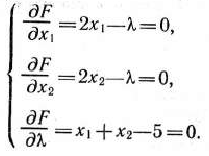
Из первого и второго уравнений имеем 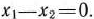 Решая это уравнение совместно с третьим из системы (23), находим
Решая это уравнение совместно с третьим из системы (23), находим 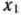 = 5/2;
= 5/2; 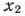 = 5/2. Таким образом, в точке (5/2; 5/2) данная функция может иметь условный экстремум. Чтобы определить, достигается ли в этой точке условный экстремум, нужно провести дополнительные исследования. В частности, используя вторые частные производные, можно показать, что в этой точке функция имеет условный минимум и
= 5/2. Таким образом, в точке (5/2; 5/2) данная функция может иметь условный экстремум. Чтобы определить, достигается ли в этой точке условный экстремум, нужно провести дополнительные исследования. В частности, используя вторые частные производные, можно показать, что в этой точке функция имеет условный минимум и
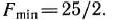
Метод множителей Лагранжа можно применять и в том случае, когда условия связи представляют собой неравенства. Так, если требуется найти экстремум функции 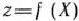 при условии
при условии 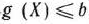 , то сначала следует найти точки безусловного экстремума функции
, то сначала следует найти точки безусловного экстремума функции 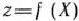 из уравнений
из уравнений
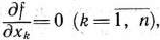
затем среди этих точек отобрать те, координаты которых удовлетворяют условию связи 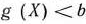 , и, наконец, определить точки, удовлетворяющие системе уравнений
, и, наконец, определить точки, удовлетворяющие системе уравнений
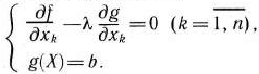
Точки, найденные в результате решения этой системы, вместе с точками, определенными на первом этапе и удовлетворяющими условию 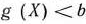 , подлежат дальнейшему исследованию, как и при нахождении безусловного экстремума.
, подлежат дальнейшему исследованию, как и при нахождении безусловного экстремума.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:

