Задача 1.43.
Найти решение задачи, состоящей в определении максимального значения функции
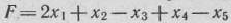
при условиях
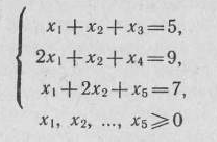
и дать геометрическую интерпретацию процесса решения.
Решение:
Систему уравнений задачи запишем в векторной форме:
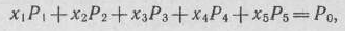
где
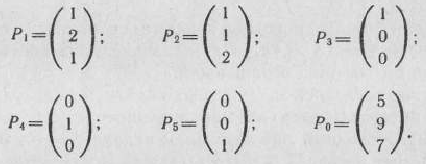
Так как среди векторов
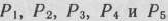
имеется три единичных вектора
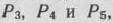
то для данной задачи можно непосредственно написать опорный план и, следовательно, найти ее решение симплексным методом (табл. 1.12).
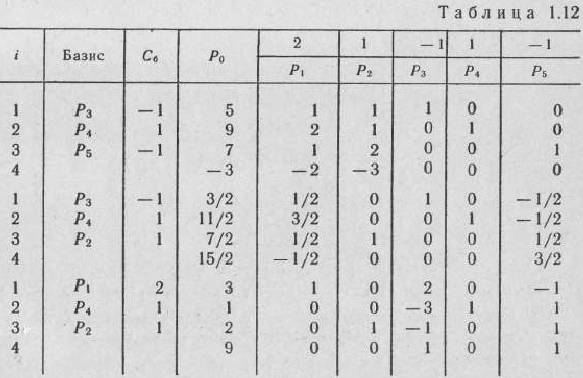
Из табл. 1.12 видно, что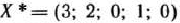 
является оптимальным планом исходной задачи. При этом плане значение линейной формы равно 
.
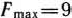Дадим геометрическую интерпретацию процесса нахождения решения задачи. Для этого прежде всего перейдем от исходной задачи, система ограничений которой содержит уравнения, к задаче, система ограничений которой включает лишь неравенства. Это сделать нетрудно, так как исходная задача записана в форме основной для задачи, состоящей в нахождении максимального значения функции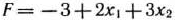 
при условиях
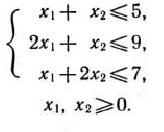
Целевая функция исходной задачи преобразована с помощью подстановки вместо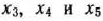 
их значений в соответствии с уравнениями системы ограничений.
Решение последней задачи можно найти, используя геометрическую интерпретацию задачи линейного программирования (рис. 1.9). Исходный опорный план задачи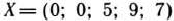 
соответствует на рис. 1.9 точке О. После II итерации был получен новый опорный план 
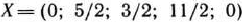, которому соответствует точка 
. На рисунке переход от одного опорного плана к другому показан стрелкой, указывающей направление
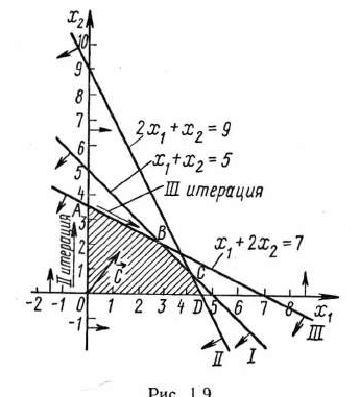
перехода. После III итерации получен опорный план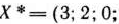 
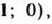, соответствующий точке 
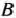, т.е. осуществлен переход от точки 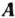к точке 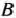. Полученный на данной итерации опорный план является оптимальным.
. Полученный на данной итерации опорный план является оптимальным.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
