Задача 2.30.
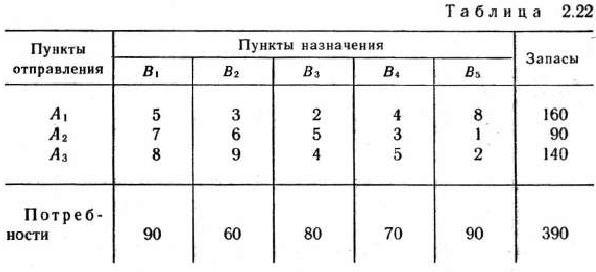
Найти решение транспортной задачи, исходные данные которой приведены в талб. 2.22, при дополнительных условиях: из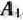 
в 
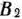должно быть перевезено не менее 50 ед. груза, из 
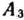в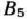 
— не менее 60 ед. груза, а из 
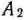в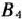 
— не более 40 ед. груза.
Решение:
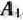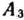Так как из и соответственно в 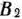и 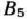необходимо завезти не менее 50 и 60 ед. груза, то запасы этих пунктов отправления и потребности пунктов назначения считаем меньшими соответственно на 50 и 60 ед. (табл. 2.23). Кроме того, поскольку из 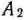в 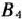необходимо завезти не более 40 ед. груза, то рассмотрим дополнительный пункт назначения 
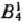с потребностями, равными 70—40 = 30 ед., а потребности пункта 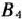считаем равными 40 ед. В столбце 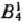записываем тарифы, помещенные в клетках столбца за исключением клетки 
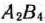. В этой клетке тариф полагаем равным некоторому сколь угодно большому числу 
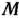. В результате получаем транспортную задачу, исходные данные которой записаны в табл. 2.23.
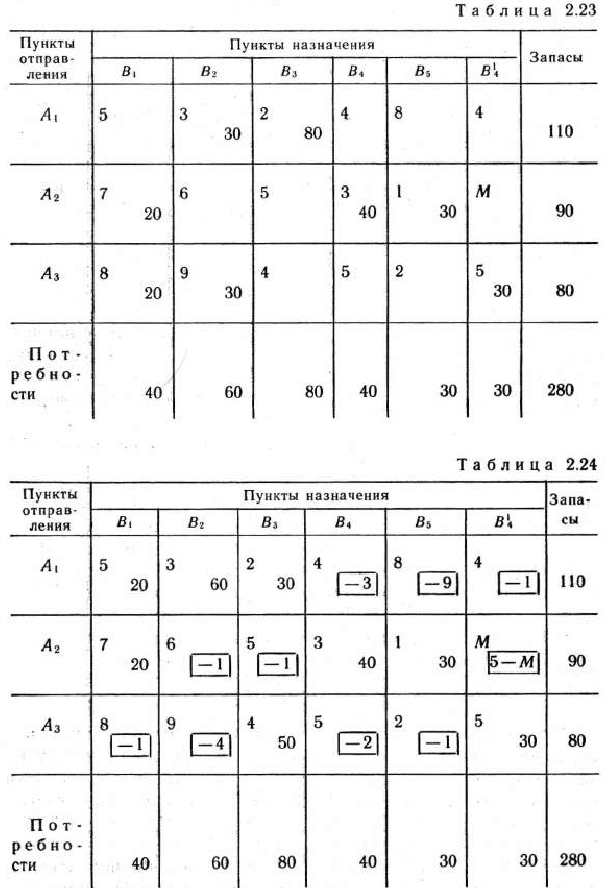
Данную задачу решаем методом потенциалов. Найденное решение приведено в табл. 2.24. Как следует из этой таблицы, оптимальное решение исходней задачи
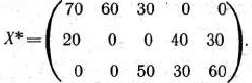
При таком плане перевозок общая стоимость перевозок
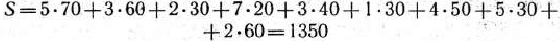
является минимальной.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
