Задача 2.29.
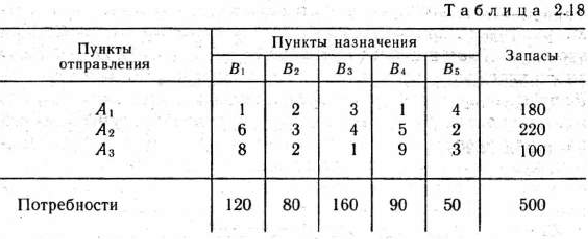
Найти решение транспортной задачи, исходные данные которой приведены в табл. 2.18, при дополнительных условиях: из 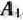 в
в 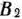 и из
и из 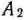 в
в 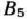 перевозки не могут быть осуществлены, а из
перевозки не могут быть осуществлены, а из 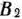 в
в 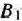 будет завезено 60 ед. груза.
будет завезено 60 ед. груза.
Решение:
Так как из 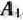 в
в 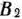 и из
и из 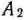 в
в 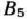 перевозки не могут быть осуществлены, то в клетках
перевозки не могут быть осуществлены, то в клетках 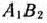 и
и 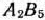 табл. 2.19 тарифы считаем равными некоторому сколь угодно большому числу
табл. 2.19 тарифы считаем равными некоторому сколь угодно большому числу 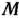 . Полагаем равным этому же числу и тариф для клетки
. Полагаем равным этому же числу и тариф для клетки 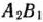 . Одновременно в эту клетку помещаем число 60, поскольку, по условию, из
. Одновременно в эту клетку помещаем число 60, поскольку, по условию, из 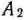 в
в 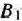 нужно завести 60 ед. груза. В дальнейшем клетку
нужно завести 60 ед. груза. В дальнейшем клетку 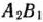 считаем свободной со сколь угодно большим тарифом
считаем свободной со сколь угодно большим тарифом 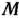 .
.

Для транспортной задачи, исходные данные которой записаны в табл. 2.19, методом минимального элемента находим опорный план. Этот план проверяем на оптимальность. Для каждого из пунктов отправления и назначения находим потенциалы, а для каждой из свободных клеток — числа
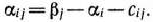
Эти числа записываем в квадратах в соответствующих клетках табл. 2,19. Если среди данных чисел нет положительных, то найденный опорный план является оптимальным. В данном случае имеется два положительных числа, расположенных в клетках 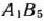 и
и 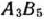 . Поэтому переходим к новому опорному плану. Строим для клетки
. Поэтому переходим к новому опорному плану. Строим для клетки 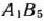 цикл пересчета и производим сдвиг по циклу пересчета (табл. 2.20).
цикл пересчета и производим сдвиг по циклу пересчета (табл. 2.20).
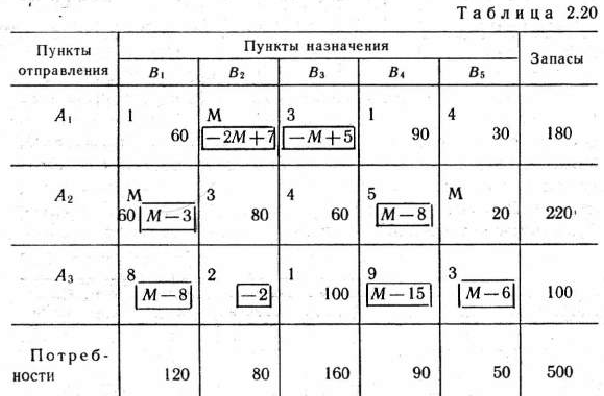
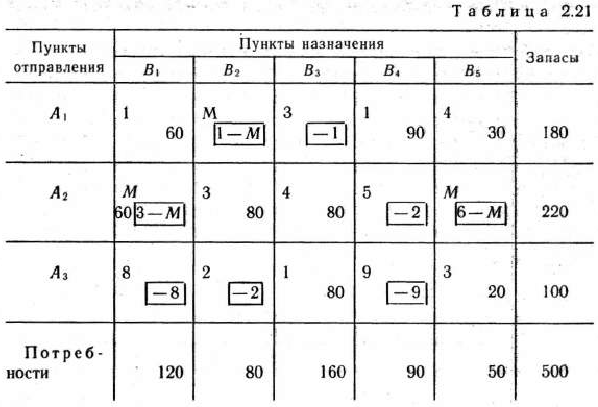
Полученный опорный план проверяем на оптимальность; так как он не оптимален, то переходим к новому опорному плану (табл. 2.21).
Как видно из табл. 2.21, исходная транспортная задача имеет оптимальный план

При этом общая стоимость перевозок
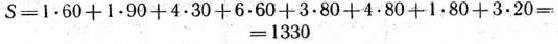
является минимальной.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:

