Задача 1.88.
Найти решение двойственной пары задач.
Исходная задача:
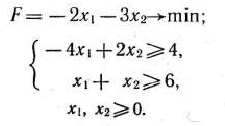
Двойственная задача:
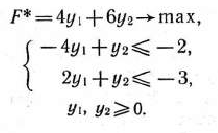
Решение:
Как исходная, так и двойственная задача содержат по две переменные. Поэтому их решение находим, используя геометрическую интерпретацию задачи линейного программирования (рис. 1.16 и 1.17). Из рис. 1.16 видно, что исходная задача не имеет оптимального плана из-за неограниченности снизу ее целевой функции на множестве допустимых решений.
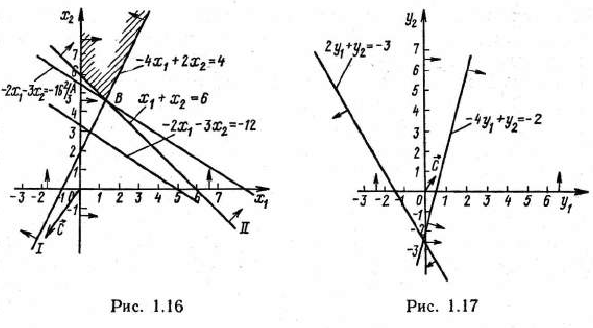
Из рис. 1.17 следует, что двойственная задача не имеет планов, поскольку многоугольник решений ее пуст. Это означает, что если исходная задача двойственной нары не имеет оптимального плана из-за неограниченности на множестве допустимых решений ее целевой функции, то двойственная задача также не имеет планов.
Нахождение решения двойственных задач. Рассмотрим пару двойственных задач — основную задачу линейного программирования (61) — {63) и двойственную к ней задачу (64), (65).
Предположим, что с помощью симплексного метода найден оптимальный план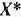 
задачи (61) — (63) и этот план определяется базисом, образованным векторами
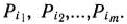
Обозначим через
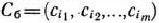
вектор-строку, составленную из коэффициентов при неизвестных в целевой функции (61) задачи (61) — (63), а через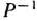 
матрицу, обратную матрице Р, составленной из компонент векторов 
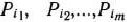, базиса. Тогдя имеет место следующее утверждение.
Теорема 1.! 1. Если основная задача линейного программирования имеет оптимальный план 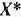, то 
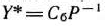является оптимальным планом двойственной задачи.
Таким образом, если найти симплексным методом оптимальный план задачи (61) — (63), то, используя последнюю симплекс-таблицу, можно определить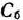 
и 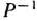и с помощью соотношения 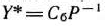найти оптимальный план двойственной задачи (64), (65).
В том случае, когда среди векторов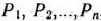 
, составленных из коэффициентов при неизвестных в системе уравнений (62) имеется 
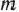единичных, указанную матрицу 
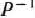образуют числа первых 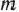строк последней симплекс-таблицы, стоящие в столбцах данных векторов, Тогда нет необходимости определять оптимальный план двойственной задачи умножением 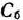на 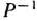поскольку компоненты этого плана совпадают с соответствующими элементами 
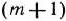-й строки столбцов единичных векторов, если данный коэффициент 
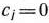, и равны сумме соответствующего элемента этой строки и 
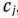, если 
.
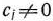Сказанное выше имеет место и для симметричной пары двойственных задач. При этом так как система ограничений исходной задачи содержит неравенства вида то компоненты оптимального плана двойственной задачи совпадают с соответствующими числами 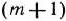-й строки последней симплекс-таблицы решения исходной задачи. Указанные числа стоят в столбцах векторов, соответствующих дополнительным переменным.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
