Задача 1.48.
Найти модифицированным симплекс-методом решение задачи 1.46, состоящей в определении максимального значения функции
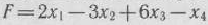
при условиях
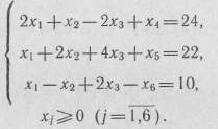
Решение:
Для сформулированной задачи нельзя непосредственно написать опорный план. Поэтому рассмотрим расширенную задачу: найти максимум функции
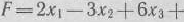

при условиях
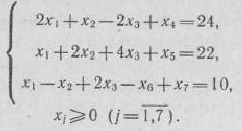
Расширенная задача имеет опорный план 
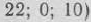 , который определяется базисом, образованным векторами
, который определяется базисом, образованным векторами 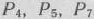 . Так как эти векторы единичные, то матрица, составленная из компонент этих векторов
. Так как эти векторы единичные, то матрица, составленная из компонент этих векторов 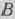 , и обратная к ней
, и обратная к ней 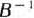 являются единичными.
являются единичными.
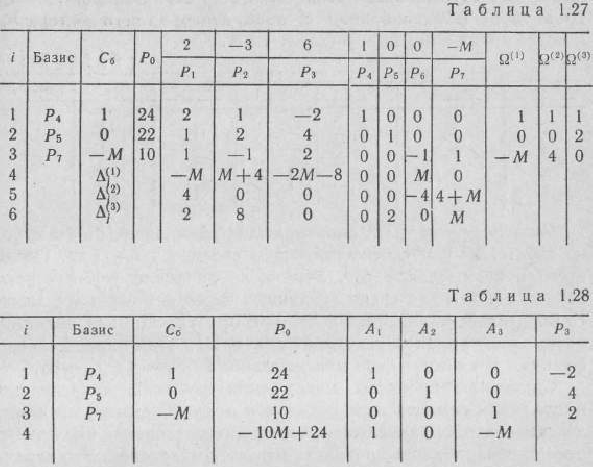
Составляем вспомогательную и основную таблицы (табл. 1.27 и 1.28). Затем находим компоненты вектора 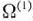 записываем их в 4-й строке табл. 1.28 и в соответствующем столбце табл. 1.27. После этого находим числа записываем их в 4-й строке табл. 1.27. Так как под
записываем их в 4-й строке табл. 1.28 и в соответствующем столбце табл. 1.27. После этого находим числа записываем их в 4-й строке табл. 1.27. Так как под 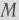 понимается некоторое сколь угодно большое положительное число, то среди чисел
понимается некоторое сколь угодно большое положительное число, то среди чисел 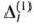 есть два отрицательных: —
есть два отрицательных: — 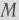 и — 2
и — 2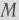 — 8. Наибольшее по абсолютной величине отрицательное число находится в столбце вектора
— 8. Наибольшее по абсолютной величине отрицательное число находится в столбце вектора 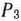 . Поэтому в последнем столбце табл. 1.28 записываем компоненты разложения вектора
. Поэтому в последнем столбце табл. 1.28 записываем компоненты разложения вектора 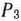 по векторам данного базиса. Вводя в базис вектор
по векторам данного базиса. Вводя в базис вектор 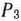 и исключая из него вектор
и исключая из него вектор 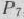 , переходим к новому опорному плану (табл. 1.29).
, переходим к новому опорному плану (табл. 1.29).
Найденный опорный план
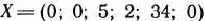
проверяем на оптимальность. Для этого находим вектор 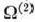 и определяем числа
и определяем числа 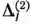 . Так как среди этих чисел есть отрицательные (—4), то в табл. 1.29 заполняем столбец вектора
. Так как среди этих чисел есть отрицательные (—4), то в табл. 1.29 заполняем столбец вектора 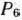 и переходим к новому опорному плану (табл. 1.30).
и переходим к новому опорному плану (табл. 1.30).
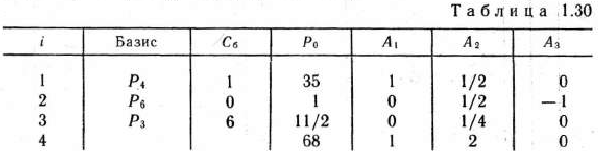
Находим вектор 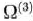 , записываем его компоненты в 4-й строке табл. 1.30 и в соответствующем столбце табл. 1.27. После этого находим числа
, записываем его компоненты в 4-й строке табл. 1.30 и в соответствующем столбце табл. 1.27. После этого находим числа 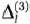 . Эти числа записаны в 6-й строке табл. 1.27. Так как среди указанных чисел нет отрицательных, то найденный опорный план
. Эти числа записаны в 6-й строке табл. 1.27. Так как среди указанных чисел нет отрицательных, то найденный опорный план 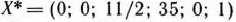 является оптимальным планом исходной задачи. При этом плане целевая функция принимает свое максимальное значение
является оптимальным планом исходной задачи. При этом плане целевая функция принимает свое максимальное значение 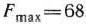 .
.
Сравнивая процессы нахождения решения приведенных выше задач симплексным методом и модифицированным симплексным методом, заключаем, что при использовании последнего метода понадобилось проводить меньше вычислений. Это характерно и для нахождения решения других задач линейного программирования, прежде всего таких, для которых число 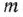 существенно меньше, нежели
существенно меньше, нежели 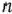 . Поэтому во многих случаях при выборе метода решения конкретных задач предпочтение отдается модифицированному симплексному методу. При этом для различных форм этого метода разработаны стандартные программы его использования при решении конкретных задач на ЭВМ.
. Поэтому во многих случаях при выборе метода решения конкретных задач предпочтение отдается модифицированному симплексному методу. При этом для различных форм этого метода разработаны стандартные программы его использования при решении конкретных задач на ЭВМ.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:

