Задача 1.45.
Найти минимум функции
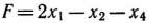
при условиях
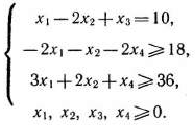
Решение:
Запишем данную задачу в форме основной задачи линейного программирования: найти максимум функции
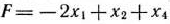
при условиях
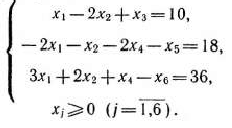
Так как среди векторов
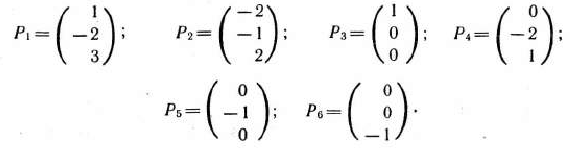
имеется только один единичный 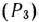 , то находим решение расширенной задачи, состоящей в определении максимального значения функции
, то находим решение расширенной задачи, состоящей в определении максимального значения функции
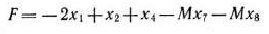
при условиях

Расширенная задача имеет опорный план
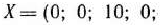
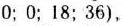
определяемый системой трех единичных векторов:
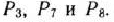
Составляем таблицу I итерации.
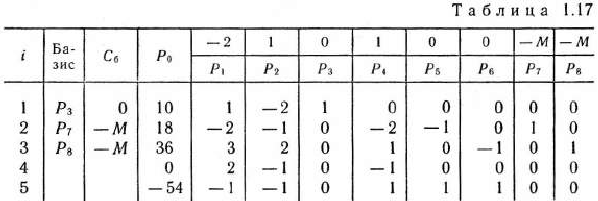
В 5-й строке табл. 1.17 в столбцах векторов 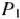 и
и 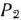 имеются отрицательные числа. Поэтому переходим к новому опорному плану расширенной задачи. В базис вводим вектор
имеются отрицательные числа. Поэтому переходим к новому опорному плану расширенной задачи. В базис вводим вектор 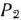 , а из базиса исключаем вектор
, а из базиса исключаем вектор 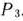 .
.
Составляем таблицу II итерации (табл. 1.18). Так как исключенный из базиса искусственный вектор 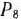 не имеет смысла вводить ни в один из последующих базисов, то в таблице этот вектор не указывается.
не имеет смысла вводить ни в один из последующих базисов, то в таблице этот вектор не указывается.
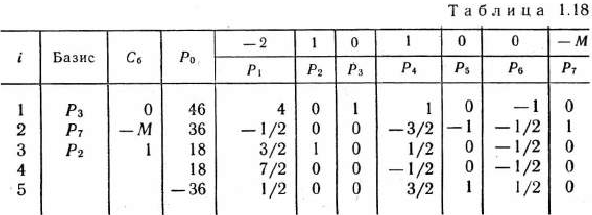
В 5-й строке табл. 1.18 в столбцах векторов
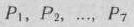
не содержится отрицательных элементов. В столбце же вектора 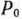 этой строки находится отрицательное число (—36). Следовательно, исходная задача не имеет опорного плана.
этой строки находится отрицательное число (—36). Следовательно, исходная задача не имеет опорного плана.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:

