Задача 1.44.
Найти минимум функции
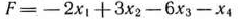
при условиях
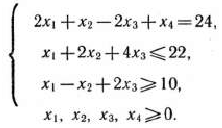
Решение:
Запишем данную задачу в форме основной задачи: найти максимум функция
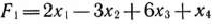
при условиях
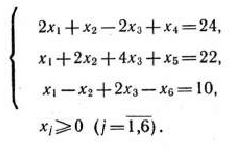
В системе уравнений последней задачи рассмотрим векторы из коэффициентов при неизвестных:
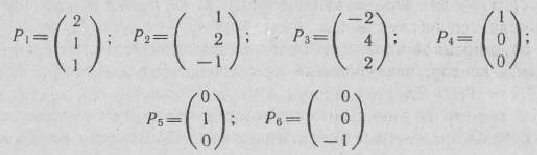
Среди векторов 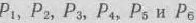 только два единичных
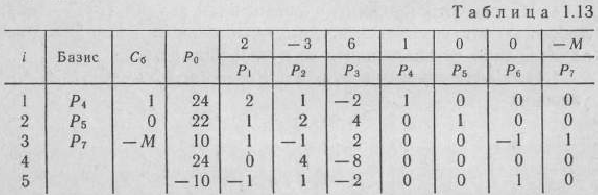
только два единичных 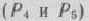 . Поэтому в левую часть третьего уравнения системы ограничений задачи добавим дополнительную неотрицательную переменную
. Поэтому в левую часть третьего уравнения системы ограничений задачи добавим дополнительную неотрицательную переменную 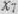 и рассмотрим расширенную задачу, состоящую в максимизации функции
и рассмотрим расширенную задачу, состоящую в максимизации функции
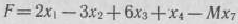
при условиях
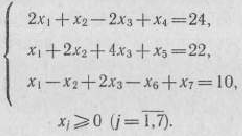
Расширенная задача имеет опорный план
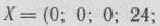
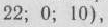
определяемый системой трех единичных векторов:
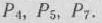
Составляем таблицу 1 итерации (табл. 1.13), содержащую пять строк. Для заполнения 4-й и 5-й строк находим 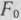 и значения разностей
и значения разностей 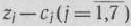 :
:
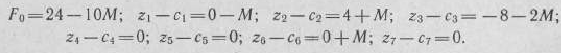
Значения 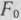 и
и  состоят из двух слагаемых, одно из которых содержит
состоят из двух слагаемых, одно из которых содержит 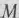 , а другое — нет. Для удобства итерационного процесса число, состоящее при
, а другое — нет. Для удобства итерационного процесса число, состоящее при 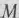 , записываем в 5-й строке, а слагаемое, которое не содержит
, записываем в 5-й строке, а слагаемое, которое не содержит 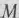 ,— в 4-й строке.
,— в 4-й строке.
В 5-й строке табл. 1.13 в столбцах векторов 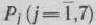 имеется два отрицательных числа (—1 и —2). Наличие этих чисел говорит о той, что данный опорный план расширенной задачи не является оптимальным. Переходим к новому опорному плану расширенной задачи. В базис вводим вектор
имеется два отрицательных числа (—1 и —2). Наличие этих чисел говорит о той, что данный опорный план расширенной задачи не является оптимальным. Переходим к новому опорному плану расширенной задачи. В базис вводим вектор 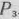 . Чтобы определить вектор, исключаемый из базиса, находим
. Чтобы определить вектор, исключаемый из базиса, находим 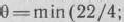
 Следовательно, вектор
Следовательно, вектор 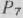 исключаем из базиса. Этот вектор не имеет смысла вводить ни в один из последующих базисов, поэтому в дальнейшем столбец данного вектора не заполняется (табл. 1.14 и 1.15).
исключаем из базиса. Этот вектор не имеет смысла вводить ни в один из последующих базисов, поэтому в дальнейшем столбец данного вектора не заполняется (табл. 1.14 и 1.15).
Составляем таблицу II итерации (табл. 1.14). Она содержит только четыре строки, так как искусственный вектор из базиса исключен.

Как видно из табл. 1.14, для исходной задачи опорным является план  . Проверим его на оптимальность. Для этого рассмотрим элементы 4-й строки. В этой строке в столбце вектора
. Проверим его на оптимальность. Для этого рассмотрим элементы 4-й строки. В этой строке в столбце вектора 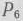 имеется отрицательное число (—4). Следовательно, данный опорный план не является оптимальным и может быть улучшен благодаря введению в базис вектора
имеется отрицательное число (—4). Следовательно, данный опорный план не является оптимальным и может быть улучшен благодаря введению в базис вектора 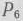 . Из базиса исключается вектор
. Из базиса исключается вектор 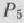 . Составляем таблицу 111 итерации.
. Составляем таблицу 111 итерации.
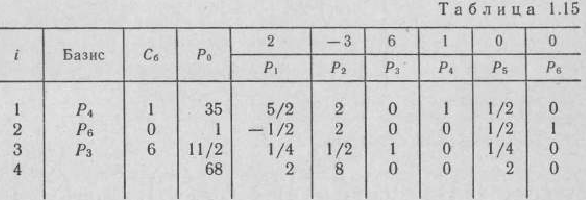
В 4-й строке табл. 1.15 среди чисел  нет отрицательных. Это означает, что найденный новый опорный план исходной задачи
нет отрицательных. Это означает, что найденный новый опорный план исходной задачи 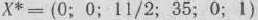 является оптимальным. При этом плане значение линейной формы
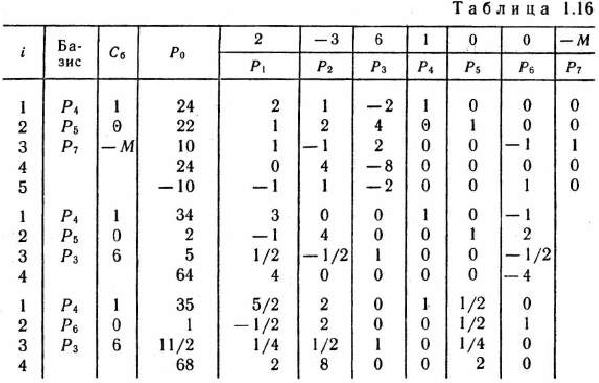
является оптимальным. При этом плане значение линейной формы 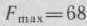 . Решение данной задачи можно было бы проводить, используя одну таблицу (табл. 1.16), а которой последовательно записаны все три итерации.
. Решение данной задачи можно было бы проводить, используя одну таблицу (табл. 1.16), а которой последовательно записаны все три итерации.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
| Задача 1.42. Найти максимум функции |
| Задача 1.43. Найти решение задачи, состоящей в определении максимального значения функции |
| Задача 1.45. Найти минимум функции |
| Задача 1.46. Найти максимум функции |

