Задача 3.4.
Найти максимальное значение функции
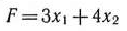
при условиях
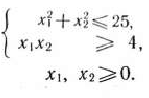
Решение:
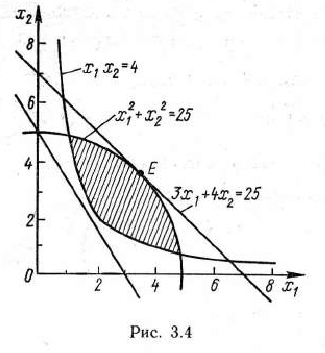
Область решений задачи (13) —(15) изображена на рис. 3.4. На этом рисунке построены две линии уровня, представляющие собой прямые. Из рис. 3.4 видно, что максимальное значение целевая функция задачи принимает в точке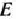 
, в которой прямая касается окружности
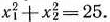
Для определения координат точки 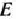воспользуемся равенством угловых коэффициентов прямой
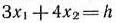
(где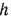 
— некоторая постоянная) и касательной к окружности в точке 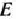. Рассматривая 
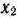как неявную функцию переменной 
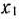, почленно дифференцируем уравнение окружности
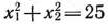
и получим
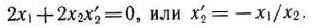
Приравнивая найденное выражение числу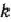 
= — 3/4, получаем одно из уравнений для определения координат точки 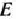. В качестве второго уравнения возьмем уравнение окружности. Таким образом, для определения координат точки 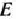имеем систему
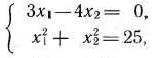
откуда
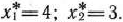
Значит,
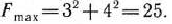
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
