Задача 3.1.
Найти максимальное значение функции
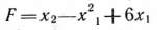
при условиях
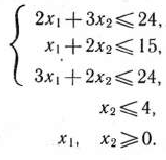
Решение:
Так как целевая функция (3) нелинейная, то задача (3)-(5) является задачей нелинейного программировании. Областью допустимых решений данной задачи является многоугольник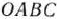 
(рис. 3.1). Следовательно, для нахождения ее решения нужно определить такую точку многоугольника 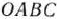, в которой функция (3) принимает максимальное значение. Построим линию уровня
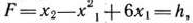
где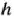 
— некоторая постоянная, и исследуем ее поведение при различных значениях 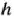. При каждом значении 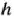получаем параболу, которая тем выше отдалена от оси 
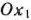, чем больше значение 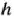(рис. 3.1). Значит, функция 
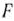принимает максимальное значение в точке касания одной из парабол с границей многоугольника 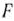. В данном случае это точка 
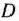(рис. 3.1), в которой линия уровня
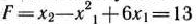
касается стороны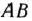 
многоугольника 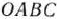. Координаты точки 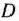можно найти из системы уравнений
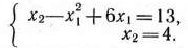
Решая эту систему, получим
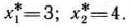
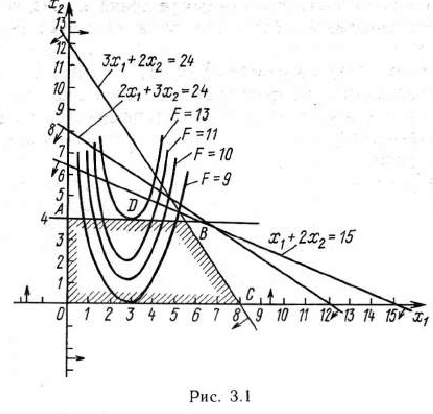
Итак,
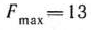
при
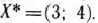
Как видим, в задаче (3) —(5) точка максимального значения целевой функции не является вершиной многоугольника решений. Поэтому процедура перебора вершин, которая использовалась при решении задач линейного программировании, неприменима для решения данной задачи.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
