Наилучшие несмещенные оценки в непрерывной модели

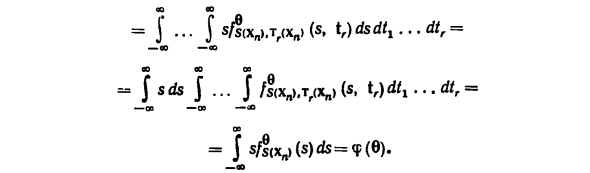
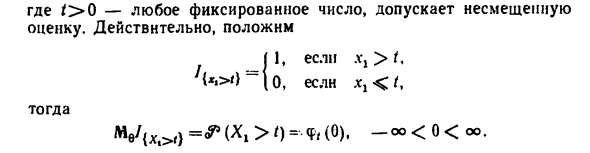
Наилучшие несмещенные оценки в непрерывной модели

• Для непрерывных моделей (/?, 3 & n, {Po.Wave}) Рассмотрим только такую ​​достаточную статистику Tj (xn) = = G «, (xn) Tr (xn)) такая карта ; = 7 \ — (xn), i = \ r Может быть дополнено некоторой статистикой Yn-r (xn) = (Y \ (xn), …, • .., Uy-g (Chl)) для преобразования один в один В пространстве R (возможно, за исключением множества P ^ -измерений ноль), Это преобразование является регулярным и может быть выполнено как обычно Изменение переменных интегрирования (см. §16). 164 Изучение различных несмещенных оценок параметра S (xn) Параметрическая функция φ ()) (T ,, s) = (T, (xn), S (xn)) /? Вся трансформация.

Теорема 3. Сделать Tx (xn) достаточной статистикой непрерывно Непрерывная модель (Rn, Rn, {P «.bev}), S (xn) -смещенная Оценка ΦF) и пары Γ (χ)), o (x)) Сформулированное выше условие регулярности. Put 00 = \ sf (s \ r) ds, C2) -CO Где условная плотность f (s \ t,) определяется уравнением C1). тогда Статистика? (Tg (x „)) φF оценивается справедливо: DQg (Tr (,)) (8)) + -f (tf (tr) — «P (e)) *] / (s | tr) ds. C6) Учитывая C2), интеграл от среднего члена C6) инвертирован В ноль. Подстановка С6) в С5) дает De (S (Xn)). = Deg (Tg (Xn)) + Me (S (Xn) -g (T, (Xn))), C7) Неравенство C3) следует.

Из определения достаточности T (xn) Условная плотность / Sxn> iW (s | tr) = / (s | tr) C1) Независимо от 0. Людмила Фирмаль

Наконец, статистика Если Tr (xn) является совершенным, решение уравнения C4) по существу Уникальная, несмещенная оценка выражения S (xn) С1) и с2) определяют по существу одну и ту же функцию g (tr), Следовательно, дисперсия оценки ^ (TG (Xn)) минимальна. Примечания 1. Tr (xn) является достаточной статистической величиной, Y (xn) — карта (tr, y) — (Tr (xn) t Y (xn)) можно добавить ко всем повторяющимся преобразованиям «. Несмещенная оценка A (Y (x ())) не обязательно Например, плотность принимает только дискретные значения. преимущества Глядя на доказательство теоремы 3, Сохраняется, когда S (x ,,) заменяется на A (Y (xl)). 8 ()) = НУ) / y (Xn> | tr (Xn) (Y | tr) dy, C8)

Поэтому теорема 3 справедлива для всех статистик. Указанная форма A (Y (Xn)). Замечания 2. Как и в индивидуальном случае, Статистика g (T, (xn)), определенная в C2) или C8), называется Условное ожидание, S (xn) или A (Y (xn)) при условии статистического Tr (xn). Спецификация: Я (S (xn) | Tr (xn)) или luMPXnJTLx))) — ¦ Используйте теорему 3, чтобы получить оценку для примера (I). Е) самый лучший. Повторная выборка в примере (III)

• Распределение с плотностью o exp (oc1 (t-t)), *> t, наибольшее Линейная несмещенная оценка σ и µ, полученная в §11, имеет вид Лучший во всех рейтинговых классах. То же самое относится Для повторного отбора проб из распределения N (μ, o2): образец Среднее и дисперсия являются наиболее справедливыми оценками. да Рассмотрим дополнительный пример. (Vii) Нормальная линейная модель в общем виде: fdy’a (y) — = (Vbio) -exp (-L-Hy-eX’H *) C9) Матрица полного ранга X приведена с использованием невырожденного Невырожденное невырожденное линейное преобразование переменной y и невырожденное

Линейное преобразование вектора параметров 6 в канонизацию Форма (см. Пункт 5 §10, пример (V) §16): Оценка наименьших квадратов Э ,, / = 1, …, r, o2 форма (r + 1) — Измерьте достаточную статистику с моделью C9) (см. Пример (V) §16). Его полнота проистекает из полноты соответствующей оценки. В переделанной модели D0) L φ, (u) = u {, i = 1, …, r, o2 (u) = ^ -r V и . D1) я — р-рл Если r = 1, полнота статистики D1) доказана на примере (IV). для Доказательство r> \ полностью аналогично r = . так

Таким образом, линейная несмещенная оценка 0, o2 находится в §9 Обычная модель С9), оценочный минимум Дисперсия возможна для всех объективных оценочных классов Людмила Фирмаль

Оцените только расстановку наблюдений. (VIII) Как в примере (I), Распределение с плотностью exp (-0.v), .v> 0. Статистика S (xn) = = ph вполне достаточно, как показано. параметрический функция φ, F) = exp (-ε /), Где O0 — произвольное фиксированное число, допускающее непредвзятость Оценка. Я вижу II, .Vj> / ‘{> *) ~~ \ 0 if *, <*, тогда Λ = &> (X.> 0 = -Φ | @). —0о <0 <оо. 167 Следовательно, наилучшая несмещенная оценка <) / *. ! «„> (! Is) dJfi = о (S- ^ Γ2 ^ .D6) о Если s t) -O PR «0 <} =, тогда’ {«,> <) = 1. = 0 и 0 /. \ s / Наилучшая несмещенная оценка φ (@) 0 если S (xn) t. Наилучшая несмещенная оценка неизвестной функции распределения Распределение в точке t 1 —φ <F) = 1 — exp (-6 /) равно 1 — g (S (xn)).

Смотрите также:

• Примеры решения задач по статистике

Полные достаточные статистики	Байесовский подход в статистике
Наилучшие несмещенные оценки в дискретной модели	Матрицы из случайных элементов

Если вам потребуется помощь по статистике вы всегда можете написать мне в whatsapp.