Оглавление:
Наибольшее и наименьшее значения функции в замкнутой области
Пусть функция 
определена и непрерывна в ограниченной замкнутой области 
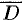. Тогда она достигает в некоторых точках 
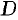своего наибольшего 
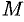и наименьшего 
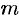значений (т. н. глобальный экстремум). Эти значения достигаются функцией в точках, расположенных внутри области 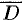, или в точках, лежащих на границе области.
Правило нахождения наибольшего и наименьшего значений дифференцируемой в области 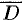функции состоит в следующем:
- Найти все критические точки функции, принадлежащие 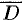, и вычислить значения функции в них;
- Найти наибольшее и наименьшее значения функции на границах области;
- Сравнить все найденные значения функции и выбрать из них наибольшее
и наименьшее .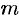
Пример №46.2.
Найти наибольшее и наименьшее значения функции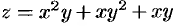 
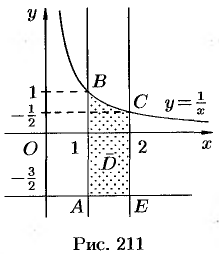
в замкнутой области, ограниченной линиями: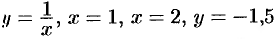 
(см. рис. 211).
Решение:
Здесь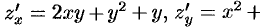 
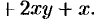
1. Находим все критические точки:
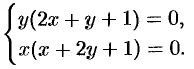
Решением системы являются точки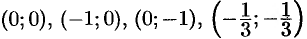 
.
Ни одна из найденных точек не принадлежит области .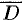
2. Исследуем функцию 
на границе области, состоящей из участков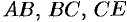 
и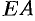 
(рис. 211).
На участк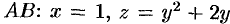е 
, где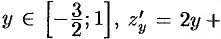 
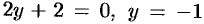. Значения функции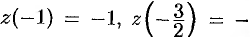 
.
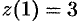На участк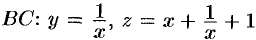е 
, где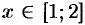 
, 
, 
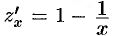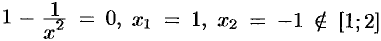. Значения функции , 
.
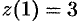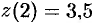На участке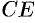 
: 
, 
, 
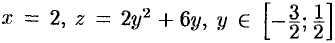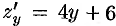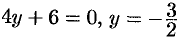. Значения функции 
.
На участке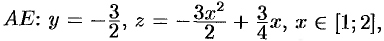 
, 
, 
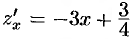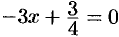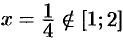. Значения функции 
.
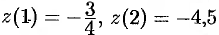3. Сравнивая полученные результаты, имеем:
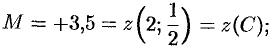
а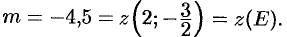 
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Касательная плоскость и нормаль к поверхности |
| Необходимые и достаточные условия экстремума |
| Задачи, приводящие к дифференциальным уравнениям |
| Уравнения с разделяющимися переменными |
