Наибольшее и наименьшее значение функции на отрезке
Согласно теореме Вейерштраса (п.3.6) непрерывная функция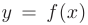 
достигает на отрезке 
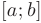своего наибольшего и наименьшего значений. Этих значений функция может достигать: а) на границах отрезка, т.е. при 
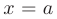или при 
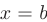: б) во внутренних критических точках, т.е. при 
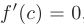, где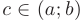 
.
Заметим, что если функция 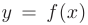имеет на отрезке 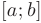лишь одну критическую точку, которая является точкой максимума (или минимума), то своего наибольшего (или наименьшего) значения на этом отрезке функция достигает именно в этой точке.
Если же функция 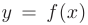на отрезке 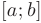вообще не имеет критических точек, то функция монотонна на этом отрезке и, следовательно, достигает своего наибольшего и наименьшего значений на концах отрезка.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Возрастание и убывание функции в математике |
| Максимум и минимум функции в математике |
| Выпуклость графика функции. Точки перегиба в математике |
| Функция многих переменных в математике |
