Оглавление:




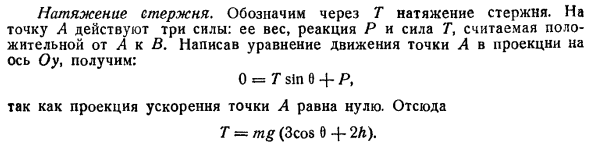

Наибольшее число независимых общих уравнений
- Для абсолютного движения мы получили 7 общих уравнений.3 проекция импульса, 3 момент импульса, 1 кинетическая энергия. Применяя теорему о моменте и кинетической энергии относительного движения вокруг центра тяжести, получаем еще 4 уравнения. Однако эти уравнения не являются независимыми от 7 общих уравнений, но, как упоминалось ранее, они приводят к тому, что в различных случаях удобнее использовать уравнение момента и кинетическую энергию для абсолютного движения или использовать эти уравнения для относительного движения вокруг центра тяжести. Любая часть system. In материальная система S, мысленно отделяющая определенную часть Р, которая образована вполне определенной материальной точкой.
Если мы рассмотрим внешнюю силу части P, действующую на оставшуюся часть P из S, то мы можем применить 7 общих уравнений. Такие соображения часто помогают найти взаимодействие и реакцию обеих частей S P и P. 354.Пример I. тяжелая система в пустоте. Когда произвольная свободная и тяжелая система брошена в пустоту, ее центр тяжести представляет собой параболу. Проведите ось в определенном направлении через центр тяжести, причем ось Gz вертикально вверх. Теорема о кинетической энергии может быть применена к относительному движению системы относительно этих осей. Внешняя сила это только сила веса, проекция веса точки м на ось движения равна 0, 0, mg.
Согласно упражнению 8 мы приходим, таким образом, к возможности приложения уравнений Лагранжа к фигуре равновесия нити. Людмила Фирмаль
У нас есть 2МВ 2 в1 ВН д 2 = т8dz + 2Д drJk Однако, поскольку начальная точка находится в центре тяжести, сумма J mz и m dz равна нулю Таким образом, кинетическая энергия относительного движения относительно оси Gx y Z изменяется только под действием внутренних сил. Если система твердая, то относительная кинетическая энергия остается постоянной. Пример II исследуют движение пустоты в двух тяжелых точках А и в одинаковой массы м. Эти точки соединены между собой упругими нитями невесомости. Предположим, что длина нити, которая не растягивается, равна 2Z, а при растяжении до длины 2 g ее натяжение пропорционально удлинению 2 g. Т = МК р л.
Когда нить растягивается до длины 2r0 2Z, обе точки выбрасываются в пустоту. Тогда центроид O, совпадающий с центром AB, описывает параболу как тяжелую точку. При относительном движении к оси Gx y z в определенном направлении через G, главный момент Ga относительно точки G числа относительного движения остается постоянным по размеру и направлению площадь 350, пример 5, и теорема является проекцией движения в каждой из 3 координатных плоскостей. Если координаты точки A обозначены через x , y , r , то координаты точки B будут x , y , z , а теорема о площади представлена 3 уравнениями. Я найду его здесь. Qx + C2y 4 C8 = 0.
Это означает, что прямая AB всегда будет оставаться в определенной плоскости II в определенном направлении через G. Эта плоскость перпендикулярна к 7a и является плоскостью максимальной площади для относительного motion. In кроме того, эта характеристика не зависит от внутренних сил, то есть от взаимодействия обеих точек. В этом случае возьмем эту плоскость плоскости x gy , среди которой 2 основания Gx , Gy выбирают определенное направление. Полярные координаты точки А этой плоскости показаны в r и 9.Координаты точки B равны r и от 0 до 4 K. форма уравнения площади имеет вид Р = С 1 Примените теорему о кинетической энергии к относительному движению вокруг центра тяжести.
Основная работа силы тяжести равна нулю пример I .Поэтому достаточно рассчитать работу натяжения обеих нитей, действующих на точки А и В. эти напряжения играют роль взаимного притяжения в обеих точках и имеют алгебраическое значение mk r I .Из за симметрии обе точки, очевидно, имеют одинаковую относительную скорость относительно оси Gx y … a mki Р Я Д 2р Потому что расстояние между точками составляет 2g. когда вы консолидируетесь, вы получаете: v, 2 = Л2 Г 4 Л 2 2 Или, если вы замените v в конце выражением в полярных координатах: Ж + Г й 3 = , г + л 2 Выражения 1 и 2 одновременно определяют r и 0 функции T.
Если желательно найти 1 относительную траекторию этих точек в плоскости П, то достаточно исключить из них dt equations. In таким образом мы получаем дифференциальное уравнение траектории у = Уду, 3 V г н Lg y G g 2 C1 значение r также увеличивается с увеличением 0 или, наоборот, уменьшается, в зависимости от того, нужно ли брать 4 или знака. Для начального значения r0 I многочлен под корнем положителен. Поскольку этот многочлен отрицателен при r = 0 и r = oo, он меньше Z, поэтому поток исчезает в линейном сегменте до тех пор, пока поток не повторится. Рисунок 196. ясно, что r должен находиться между 2 маршрутами a и, и только от одного из них к другому.
- Согласно уравнению 1, 0 всегда изменяется в одном направлении, и кривая является горизонтальной проекцией сферического маятника С. 227, аналогично кривой, описанной на рис.170. Заметим, однако, что в выражении r всегда предполагается больше Z. Если в какой то момент r равно Z, и оно не растягивается, то сила T исчезает, как k. акцент делается на независимом вращении до момента, когда начинается относительная траектория плоскости ятся, и сила t становится равной Z. stretched.
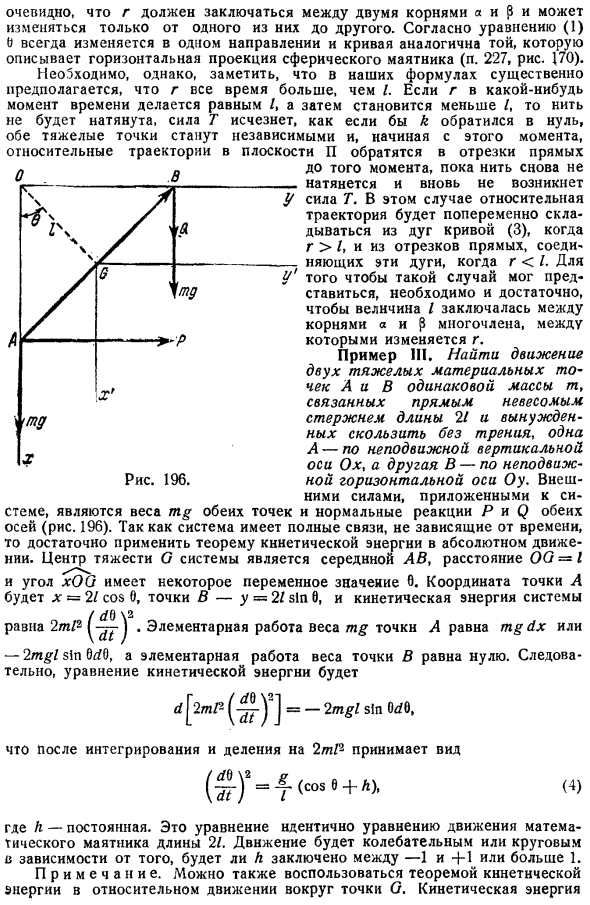
В этом случае относительная траектория суммируется поочередно от дуги кривой 3, когда r Z, и от отрезков линии, соединяющих эти дуги, когда r 1.In для того чтобы такой случай возник, необходимо и достаточно, чтобы значение Z лежало между корнями многочленов a и p, между которыми изменяется r. Пример III найти движение 2 тяжелых материальных точек А и в одинаковой массы м. Длина 21 соединена прямым невесомым стержнем и вынуждена скользить без трения.1 движется вдоль неподвижной вертикальной оси Ox, а другой 1 движется вдоль неподвижной горизонтальной оси Oy.
Это можно доказать, опираясь на результаты предыдущего упражнения, если приложить их к параболе безопасности, которая рассматривается как обобщенная развертка точки О. Людмила Фирмаль
Внешняя сила, приложенная к системе, представляет собой вес обеих точек, mg, и вертикальные силы реакции P и Q на обеих осях рис.196.Поскольку система идеально связана независимо от времени, достаточно применить теорему о кинетической энергии к абсолютному движению. Центром тяжести G системы является середина AB, расстояние OG = Z, а угол xOQ переменное значение 0.Координаты точки A равны x = 21 cos0, точки B y = 2Z sin 0, а кинетическая энергия системы равна 2 nZ2. 2mg7 sin 0 0, базовая работа веса точки B равна zero.
So уравнение кинетической энергии имеет вид Zrf0 2 1 1.Точки A, вес мг, основная работа mndx или 2Т гл грех Orf0 Формат после интегрирования и деления на 2ТП 40 2 у cos0 + л 4 Где h константа. Это уравнение совпадает с уравнением движения математического маятника длины 21.Упражнение а 1 4 он колеблется или циркулирует, в зависимости от того, равен ли он 1 или больше 1. Обратите внимание, что вы также можете использовать теорему о кинетической энергии для относительного движения вокруг G. кинетическая энергия относительного движения относительно оси Gx в постоянном направлении db 2 2mp1 явления, взятого из точки G.
Сумма весов обеих точек A и B при относительном смещении по этим осям равна нулю, но нормальные реакции P и Q при этом относительном смещении ненулевые, поэтому относительные фундаментальные смещения точек наблюдателя A и B, связанных с осью Gx, являются дугой окружности, описываемой как центр радиуса GA, и следует отметить, что точка A имеет координату относительно этих осей, которая включала бы P и Q. x = i cos0, y = i sin 0, L Также точкой B является координата ag и y , указывающая на наличие проекций 0, P и Q, 0 в силах P и Q. Для основной работы этих сил величина Pdy 4 КТ х.
Искомое уравнение кинетической энергии = Qsln 0 C0S Реакции P и Q включены в это уравнение и могут быть использованы совместно с другим уравнением для их определения. Но проще вычислить P и Q непосредственно, напнснав уравнение абсолютного движения центроида G в проекции на оси Ox и Oy. Куда 5 = i cos0, tj = I sin 0 Вычислить и заменить 2 ю производную no t от 6 и tj db 2 20 dt и dP со значениями, полученными из уравнения 4, получаем P и Q с функцией 0.Знак реакции P и Q определяет направление этих реакций. 196 окрашено так, как будто оба они положительны. Р сек резус Рассчитать и. .. получить. ДП ар Д = 2 н г грех 0 ф в COSя 2мг Р = 2 cosO s1t9.
Однако уравнение 4, после дифференцирования относительно T n, принимает вид множества редукций 0. ОД Подставляя Формулы 4 и 5 в уравнения Q = mg cos 6 3 cos 0 +2Л mg, P = mg sin 6 3 cos 0 4 2ft. 5 напряжение штанги. T показывает напряжение стержня. 3 силы действуют на точку A. Ее вес, реактивная сила P и сила T считаются положительными от A до B. если спроецировать уравнение движения точки A на ось Oy, то получим: O = T sin 0 4 P Потому что проекция ускорения точки А равна нулю.
Смотрите также:
Решение задач по теоретической механике

