Наиболее известные средние величины и соотношения между ними
Пусть даны п неотрицательных чисел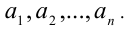 
Их средним арифметическим называется число
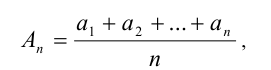
средним геометрическим — число
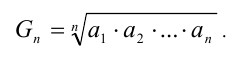
Средним гармоническим n положительных чисел 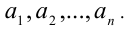называется число
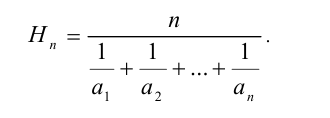
Название «среднее гармоническое» появилось в связи с исследованиями пифагорейцев в теории музыки. Они установили, что звуки, издаваемые струнами длины l и 2l , для нашего восприятия практически сливаются. Интервал, образованный этими звуками, назван октавой. А струна длины 4l/3 издает звук, образующий вместе с двумя исходными гармонично звучащий аккорд. При этом обратные величины длин струн, т.е.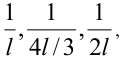 
образуют арифметическую прогрессию, так как 
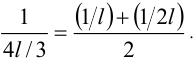По аналогии, если для чисел а,b, c выполнено равенство 
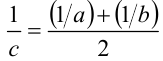, то число c стали называть средним гармоническим чисел а и b . По схожей причине числовой ряд
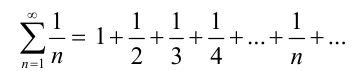
также называется гармоническим, поскольку каждый его член является средним гармоническим двух соседних членов, т.е. обратная величина любого члена равна среднему арифметическому обратных величин членов, соседних с ним:
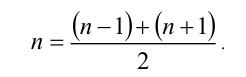
Наконец, средним квадратичным неотрицательных чисел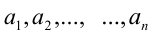 
называется число
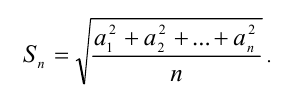
В общем случае для произвольного действительного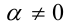 
вводится среднее степенное порядка 
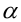для положительных чисел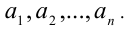
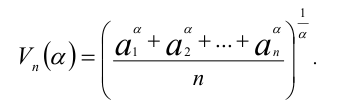
При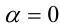 
среднее степенное определяется как 
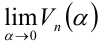. Этот предел существует и равен среднему геометрическому чисел 
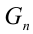. Введённые выше средние величины являются частными случаями среднего степенного. Так, при 
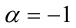среднее степенное превращается в среднее гармоническое 
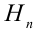, при 
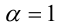из среднего степенного получаем среднее арифметическое 
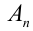, а при 
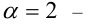среднее квадратичное 
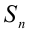. Более того, среднее степенное является возрастающей функцией параметра 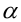, т.е. большему значению 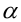всегда соответствует большее значение 
.
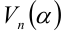На самом деле разнообразие средних величин гораздо шире. Существуют средние величины смешанного или комбинированного вида. Приведём принцип построения величин подобного рода. Пусть a и b — неотрицательные действительные числа. Рассмотрим две числовые последовательности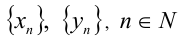 
, определяемые рекуррентными формулами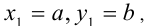 
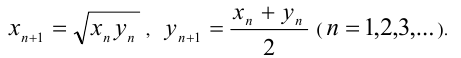
В курсе математического анализа в высших учебных заведениях доказывается, что при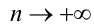 
значения 
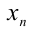и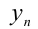 
стремятся к общему предельному значению (в школьном курсе математики, как правило, не дается строгое определение предела числовой последовательности, поэтому будем руководствоваться интуитивным понятием предельного значения). Заметим лишь, что это число существует, единственно и называется арифметико-геометрическим средним чисел a и b .
Обозначим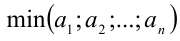 
— наименьшее, 
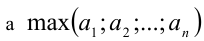— наибольшее из действительных чисел 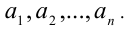. Тогда справедливо следующее соотношение между средними величинами:
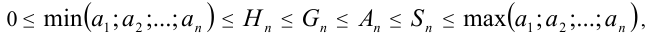
причём все неравенства одновременно обращаются в равенства тогда и только тогда, когда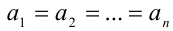 
.
В частности, для двух положительных чисел а и b имеем:
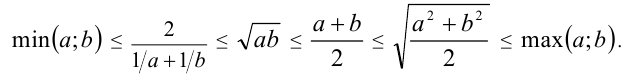
Докажем эти неравенства для случая двух чисел, сводя их эквивалентными преобразованиями к очевидным алгебраическим неравенствам.
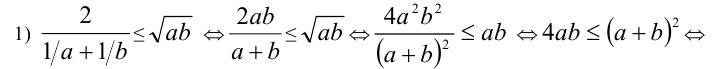
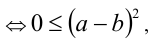причём обращаются все эти неравенства в равенства 
.
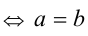2) 
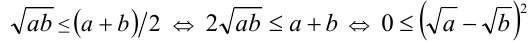, причём равенство достигается тогда и только тогда, когда а = b .
3)
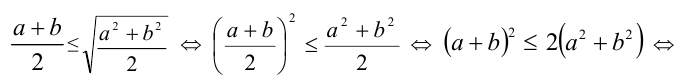
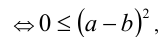причём равенство достигается .
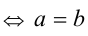Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
