Главная часть приращения функции 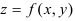 , линейная относительно
, линейная относительно 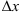 и
и 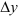 , называется полным дифференциалом этой функции и обозначается символом
, называется полным дифференциалом этой функции и обозначается символом 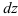 :
:
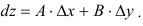
Для нахождения полного дифференциала функции 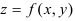 используется формула:
используется формула:
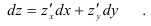
Пример решения заказа контрольной работы №82.
Найдите полный дифференциал функции
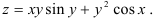
Решение:
Для нахождения полного дифференциала функции
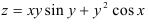
будем использовать формулу
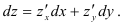
Найдём 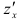 — частную производную функции по переменной
— частную производную функции по переменной 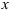 рассматривая
рассматривая 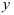 , а следовательно и
, а следовательно и 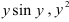 : как постоянные, применяя правило дифференцирования суммы:
: как постоянные, применяя правило дифференцирования суммы:
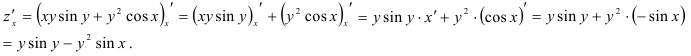
Найдём 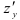 — частную производную функции по переменной
— частную производную функции по переменной 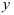 , рассматривая
, рассматривая 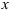 , а следовательно и,
, а следовательно и, 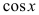 как постоянные, применяя правило дифференцирования суммы, а для дифференцирования
как постоянные, применяя правило дифференцирования суммы, а для дифференцирования 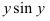 — произведения:
— произведения:
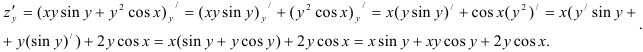
Подставим 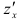 и
и 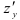 в формулу полного дифференциала, получим:
в формулу полного дифференциала, получим:
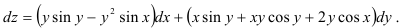
Ответ:
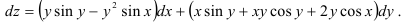
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:
| Пример вычисления подобного повторного интеграла |
| Нахождение дифференциала второго порядка функции |
| Метод интегрирования некоторых сложных функций |
| Сущность метода интегрирования подстановкой |

