Особенности нахождения оптимальных решений в задачах математического программирования
В задачах математического программирования требуется найти так называемый условный экстремум (максимум или минимум) функции при наличии ограничений. Рассмотрим задачу математического программирования, в которой есть только ограничения в виде равенств. Пусть целевая функция задачи является функцией двух переменных:
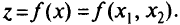
Ее аргументы связаны уравнением 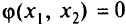 (ограничения в виде неравенств отсутствуют). Если функции
(ограничения в виде неравенств отсутствуют). Если функции 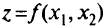 поставить в соответствие некоторую поверхность, то в данной задаче необходимо найти следующие точки:
поставить в соответствие некоторую поверхность, то в данной задаче необходимо найти следующие точки:
1) принадлежащие линии пересечения поверхности 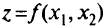 и цилиндра с образующей, параллельной оси
и цилиндра с образующей, параллельной оси 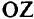 , и с направляющей
, и с направляющей 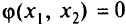 ;
;
2) в которых функция 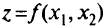 принимает экстремальные значения (рис. 1.3). Как видно из рис. 1.3, точки условного экстремума
принимает экстремальные значения (рис. 1.3). Как видно из рис. 1.3, точки условного экстремума 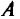 и
и 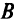 не совпадают с наибольшим или наименьшим значением функции
не совпадают с наибольшим или наименьшим значением функции 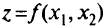 — с безусловным экстремумом функции
— с безусловным экстремумом функции 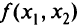 . Если из уравнения связи
. Если из уравнения связи 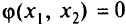 можно выразить в явном виде одну переменную через другую, например
можно выразить в явном виде одну переменную через другую, например
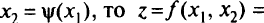
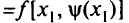
становится функцией одной переменной 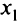 и ее безусловный экстремум отыскивается традиционными методами (приравниваем первую производную от
и ее безусловный экстремум отыскивается традиционными методами (приравниваем первую производную от 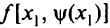 по
по 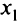 нулю).
нулю).
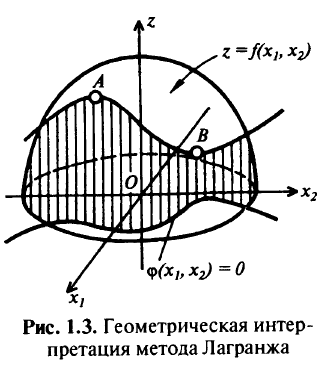
Безусловный экстремум функции 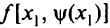 является условным экстремумом для функции
является условным экстремумом для функции 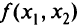 при ограничении
при ограничении 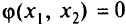 . Однако выразить в явном виде из условий-ограничений необходимую часть переменных, как правило, не удается.
. Однако выразить в явном виде из условий-ограничений необходимую часть переменных, как правило, не удается.
Лагранж предложил оригинальный метод нахождения условного экстремума функции. Метод носит его имя. Пусть требуется решить следующую задачу: минимизировать
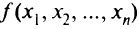
при ограничениях
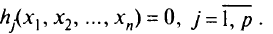
По условию задачи составляется функция Лагранжа
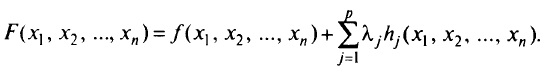
Здесь 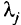 — неизвестные постоянные множители, подлежащие определению (множители Лагранжа), т.е. требуется найти
— неизвестные постоянные множители, подлежащие определению (множители Лагранжа), т.е. требуется найти 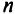 неизвестных
неизвестных 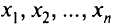 и
и 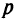 множителей Лагранжа
множителей Лагранжа 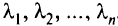 .
.
Для рассматриваемого в начале параграфа примера
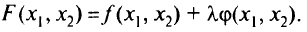
Точки, в которых возможен экстремум, находятся как решение системы алгебраических уравнений, полученной приравниванием нулю частных производных от функции Лагранжа по искомым переменным (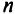 уравнений) и включением в эту систему
уравнений) и включением в эту систему 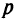 ограничений-равенств. Метод Лагранжа сводит задачу отыскан ш условного экстремума функции
ограничений-равенств. Метод Лагранжа сводит задачу отыскан ш условного экстремума функции 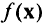 к задаче отыскания безусловного экстремума функции
к задаче отыскания безусловного экстремума функции 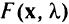 .
.
Ограничения-неравенства еще более усложняют задачу. Дело в том, что ограничения-неравенства задают область допустимых значений переменных. Например, пусть требуется оптимизировать некоторую функцию 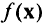 при ограничениях
при ограничениях
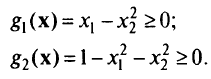
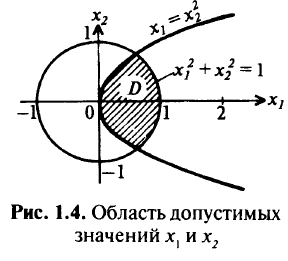
Область допустимых значений переменных 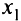 и
и 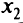 в этой задаче есть пересечение области, лежащей «внутри» параболы
в этой задаче есть пересечение области, лежащей «внутри» параболы 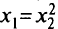 с кругом единичного радиуса, уравнение окружности которого имеет вид
с кругом единичного радиуса, уравнение окружности которого имеет вид 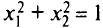 (рис. 1.4).
(рис. 1.4).
Пересечение цилиндра, направляющей которого является граница полученной области 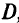 , с поверхностью
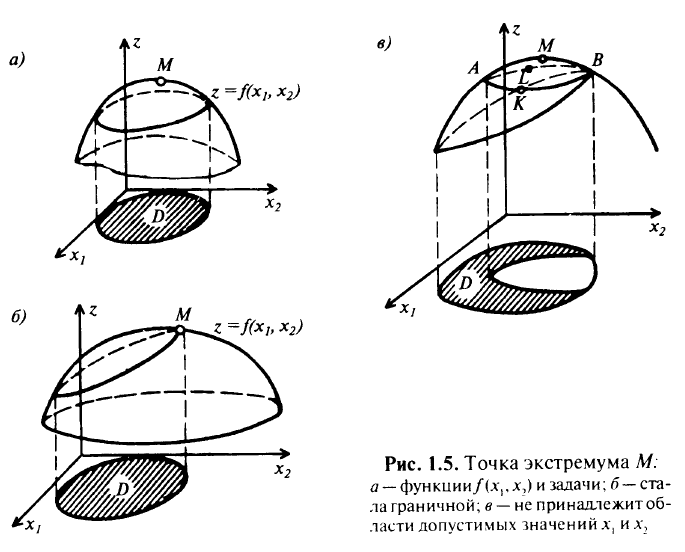
, с поверхностью 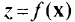 может давать самые разнообразные варианты. На рис. 1.5,я-в показаны поверхности, полученные в результате пересечения цилиндра, направляющей которого служит граница области допустимых значений переменных
может давать самые разнообразные варианты. На рис. 1.5,я-в показаны поверхности, полученные в результате пересечения цилиндра, направляющей которого служит граница области допустимых значений переменных 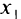 и
и 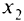 и поверхности, соответствующей целевой функции
и поверхности, соответствующей целевой функции 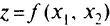 . На рис. 1.5,о точка
. На рис. 1.5,о точка 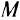 безусловного экстремума функции
безусловного экстремума функции 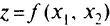 является и точкой условного экстремума задачи. На рис. 1.5,б точка
является и точкой условного экстремума задачи. На рис. 1.5,б точка 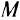 является уже граничной, и в ней целевая функция достигает своего наибольшею значения. На рис. 1.5,в точка
является уже граничной, и в ней целевая функция достигает своего наибольшею значения. На рис. 1.5,в точка 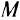 не принадлежит области допустимых значений переменных, а целевая функция имеет равные наибольшие значения полициям
не принадлежит области допустимых значений переменных, а целевая функция имеет равные наибольшие значения полициям 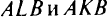 ( т.е. неясно, что же брать за решение задачи). Эти неоднозначные результаты получены даже в случае, когда поверхность целевой функции
( т.е. неясно, что же брать за решение задачи). Эти неоднозначные результаты получены даже в случае, когда поверхность целевой функции 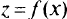 достаточно проста и обладает единственным (глобальным) максимумом.
достаточно проста и обладает единственным (глобальным) максимумом.
Наиболее полные результаты в задачах математического программирования получены для выпуклых целевых функций, когда область допустимых значений является выпуклым множеством. Множество точек 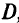 называют выпуклым, если для любых точек
называют выпуклым, если для любых точек 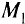 и
и 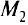 , принадлежащих области
, принадлежащих области 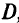 , отрезок
, отрезок 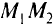 принадлежит мно-
принадлежит мно-
жеству (области) 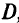 (рис. 1.6,о). Другими словами, любая точка
(рис. 1.6,о). Другими словами, любая точка 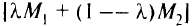 принадлежит области
принадлежит области 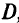 для любого
для любого 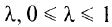 , и для любых точек
, и для любых точек 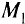 , и
, и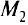 , принадлежащих области
, принадлежащих области 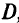 . Причем пересечение конечного числа выпуклых множеств выпукло.
. Причем пересечение конечного числа выпуклых множеств выпукло.
На рис. 1.6,б показаны невыпуклые множества. Функцию 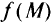 называют выпуклой на непустом выпуклом множестве
называют выпуклой на непустом выпуклом множестве 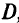 , если для любых двух точек
, если для любых двух точек 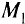 и
и 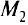 , принадлежащих области
, принадлежащих области 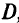 , и любого числа
, и любого числа 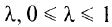 , справедливо неравенство
, справедливо неравенство
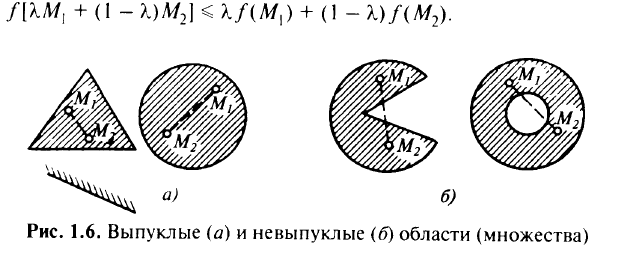
Функцию 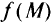 называют строго выпуклой, если для
называют строго выпуклой, если для 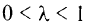 и
и 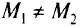 выполняется строгое неравенство
выполняется строгое неравенство
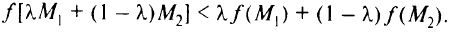
Геометрически выпуклая функция лежит надсвоими касательными. Примером выпуклой функции является парабола.
Сумма выпуклых на множестве 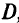 функций есть также выпуклая на
функций есть также выпуклая на 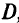 функция.
функция.
Функцию 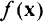 называют вогнутой на выпуклом множестве
называют вогнутой на выпуклом множестве 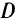 , если функция —
, если функция —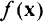 выпукла на
выпукла на 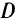 . Ограничения
. Ограничения 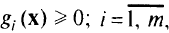 , образуют выпуклое множество
, образуют выпуклое множество 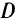 (выпуклую область
(выпуклую область 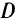 ), если все функции
), если все функции 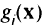 вогнуты.
вогнуты.
В математическом программировании выделяется важный класс задач — задачи выпуклого программирования: минимизировать 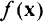 при ограничениях
при ограничениях 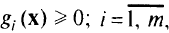 , где
, где 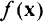 — выпуклая функция, а все функции
— выпуклая функция, а все функции 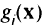 — вогнуты, т.е. рассматривают выпуклые функции на выпуклых множествах.
— вогнуты, т.е. рассматривают выпуклые функции на выпуклых множествах.
Задачи выпуклого программирования обладают важным положительным свойством: локальные минимумы целевых функций являются одновременно глобальными (единственными). Очевидно, что решить подобную задачу проще (но не просто!), чем в случае, когда целевая функция 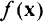 и область
и область 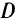 будут общего вида.
будут общего вида.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:

