Цель: формирование умения находить определённые интегралы методом подстановки.
Методические указания no выполнению работы:
Интегрирование подстановкой (заменой переменной) — осуществляется с использованием формулы
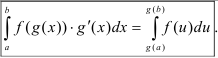
Для нахождения определенного интеграла методом подстановки (замены переменной) целесообразно использовать следующий алгоритм:
- Введите новую переменную
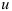таким образом, чтобы под знаком интеграла стояла функция, содержащая 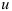(от этой функции должен существовать табличный интеграл), и производная 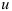. - Найдите
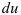по формуле: 
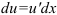. - Выразите
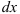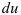через . - Найдите новые границы интегрирования
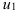и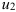 
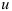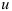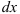, подставив исходные границы в функцию . - Подставьте и в исходный интеграл. Если подстановка выполнена верно, то произойдет сокращение одинаковых множителей и интеграл сведется к табличному относительно переменной
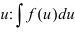. Смените границы интегрирования на 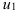и 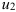. - Пользуясь таблицей неопределённых интегралов, возьмите полученный определенный интеграл с переменной .
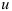Рассмотрим применение метода замены переменной на примере.
Пример решения заказа контрольной работы №71.
Вычислите
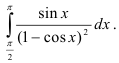
Решение:
- Выполним подстановку
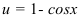с целью прийти к интегралу от функции 
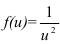. - Найдем 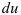по формуле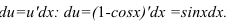
- Выразим 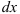из выражения пункта 2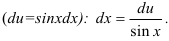
- Вычислим новые границы интегрирования для переменной 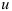. Для этого подставим существующие границы
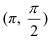в выражение 
.
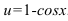Тогда нижняя граница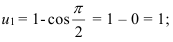 
верхняя граница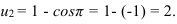 
Подставим 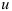и 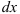в исходным интеграл (пока неопределенный):
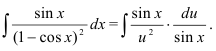
Видим, что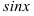 
можно сократить и прийти к интегралу относительно переменной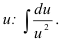 
В результате всех преобразований первоначальный интеграл примет вид: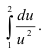 
Вычислим полученный интеграл. По таблице интегралов находим, что
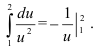
Воспользуемся свойством 3 определенного интеграла, позволяющим менять границы интегрирования, при этом избавляясь от знака «минус» перед определенным интегралом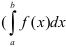 
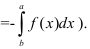
Тогда
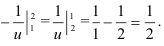
Ответ:
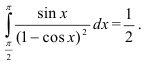
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:
