Если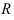 
— радиус сходимости степенного ряда 
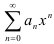, то множество точек 
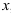, удовлетворяющих неравенству 
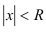, называется интервалом сходимости I степенного ряда. Значит, если 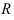— радиус сходимости степенного ряда 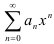, то его интервал сходимости находится следующим образом: 
.
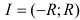Выясним, чему равен радиус сходимости данного степенного ряда. Искать его будем по соотношению: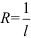 
. Для нахождения 
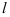применим формулу:
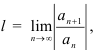
аналогичную формуле признака Даламбера. Фактически воспользуемся соответствующим алгоритмом.
Для этого: 1. найдём коэффициент
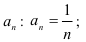
- найдём коэффициент
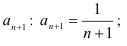
- найдём отношение коэффициентов
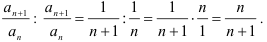
Таким образом, получим
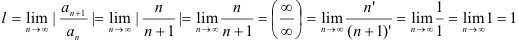
(при раскрытии неопределенности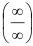 
использовали правило Лопиталя). Следовательно, так как 
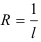, а 
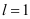, то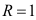 
.
Применяя формулу для нахождения интервала сходимости степенного ряда: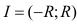 
, получим: 
.
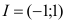Ответ: .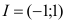
Если для степенного ряда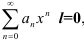 
, то его радиус сходимости 
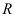равен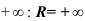 
.
Если для степенного ряда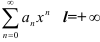 
, то его радиус сходимости 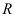равен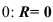 
.
Пример решения заказа контрольной работы №104.
Найдите радиус сходимости степенного ряда
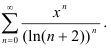
Решение:
Радиус сходимости степенного ряда
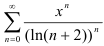
будем искать по формуле 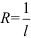. Поскольку коэффициент степенного ряда 
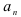представляет собой 
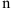— ую степень выражения
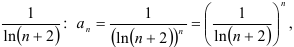
то для нахождения 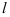применим формулу:
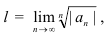
аналогичную формуле признака Коши. Фактически воспользуемся соответствующим алгоритмом. Для этого:
- найдём коэффициент
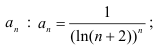
найдём
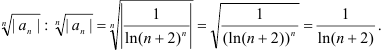
Таким образом, получим
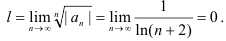
Следовательно, если
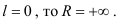
Ответ: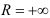 
.
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:
