Задача 2.35.
На текстильном предприятии имеется три типа ткацких станков. На станках каждого из типов могут вырабатываться четыре вида тканей: миткаль, бязь, ситец и сатин. Производительность каждого станка и себестоимость тканей приведены в табл. 2.25. Учитывая, что фонд рабочего времени каждой из групп ткацких станков соответственно равен 90, 220 и 180 станков, составить такой план их загрузки, при котором общая себестоимость
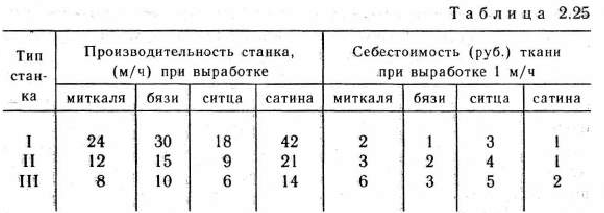
выпускаемых тканей в количестве 1200 м миткаля, 900 м бязи, 1800 м ситца и 840 м сатина является минимальной.
Решение:
Составим математическую модель задачи. Будем считать, что 
-й тип станков занят изготовлением 
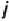-го вида тканей 
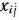станкочасов. Тогда переменные 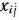должны удовлетворять следующим уравнениям:
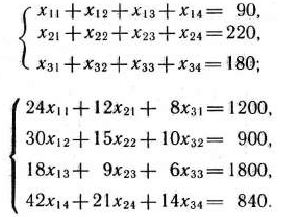
Переменные 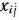должны удовлетворять также условию неотрицательности:
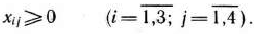
Среди всех возможных значений неизвестных 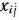удовлетворяющих уравнениям (13) и (14) и условию неотрицательности переменных (15), требуется найти такое, при котором линейная функция
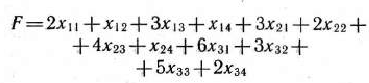
принимает наименьшее значение.
Преобразуем математическую модель задачи таким образом, чтобы свести ее к модели транспортной задачи. Для этого приведем исходные Данные и неизвестные величины исходной задачи к одной единице, в качестве которой возьмем I станко-ч работы станков I типа. Тогда, поскольку производительность станков II и III типов соответственно составляют 1/2 и 1/3 производительности станков I типа (табл, 2.25), фактический фонд рабочего времени в приведенных станко-часах для II типа станков равен 105, а для III типа — 60. Общий фонд рабочего времени в приведенных станко-часах составляет 90+105+60 = 255.
Определим теперь, какое время требуется для выработки нужного количества каждого из видов тканей. Так как нужно изготовить 1200 м миткаля и за один приведенный станко-час можно выработать 24 м, то для выпуска необходимого количества миткаля потребуется 1200/24 = 50 станко-ч. Аналогично определяем потребности для выработки бязи, ситца и сатина. Эти потребности соответственно составляют 30, 100 и 20 станко-ч. Обозначим теперь через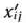 
количество приведенных станко-часов -го типа станков, используемых при выработке 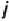-го вида ткани. Тогда системы уравнений (13) и (14) исходной задачи можно переписать так:
Целевая функция (16) исходной задачи записывается в виде
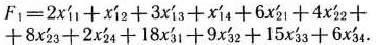
В результате приходим к следующей математической задаче: требуется среди всех неотрицательных решений систем линейных уравнений (17) и (18) найти такое, при котором функция (20) принимает минимальное значение.
Таким образом, исходная задача свелась к задаче, математическая модель которой ничем не отличается от математической модели транспортной задачи. Поскольку 90 + 105 + 60 = 225> > 50 + 30+100 + 20 = 200, полученная задача имеет открытую модель. Поэтому, чтобы найти ее решение, считаем, что имеется фиктивная потребность в тканях, на выработку которых необходимо затратить 255 — 200 = 55 станко-ч. Полученную в результате последнего предположения задачу решаем методом потенциалов (табл. 2.26).
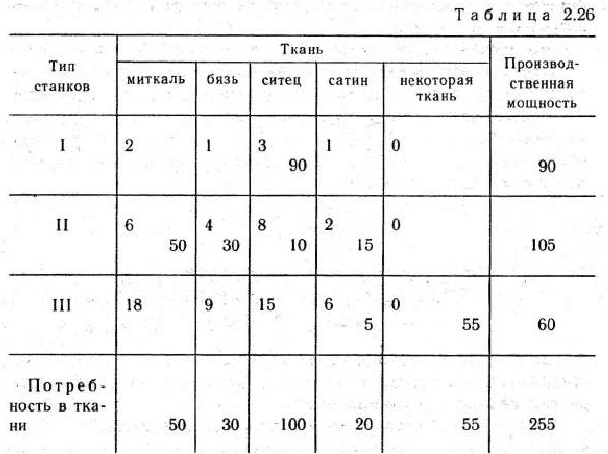
Как видно из табл. 2.26, оптимальный план задачи (17) — (20) определяется матрицей
Используя соотношения (19), для определения оптимального плана исходной задачи (13) — (16) получим матрицу
Таким образом, согласно плану выработки тканей, предусматривается использовать 90 станко-ч станков 1 типа для производства ситца, соответственно 100, 60, 20 и 30 станко-ч станков II типа для выработки миткаля, бязи, ситца и сатина, 15 станко-ч станков III типа для изготовления сатина. При этом 155 станко-ч станки 111 типа остаются свободными.
В соответствии с данным планом на станках 1 типа вырабатывается 1620 м ситца, на станках II типа — 1200 м миткаля, 900 м бязи, 180 м ситца и 630 м сатина, на станках III типа — 210 м сатина. При этом 165 станко-ч станки III типа могут быть использованы для выработки сверхплановой продукции. При данном плане выработки тканей их себестоимость является минимальной и составляет
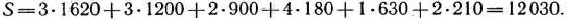
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
