Задача №101.
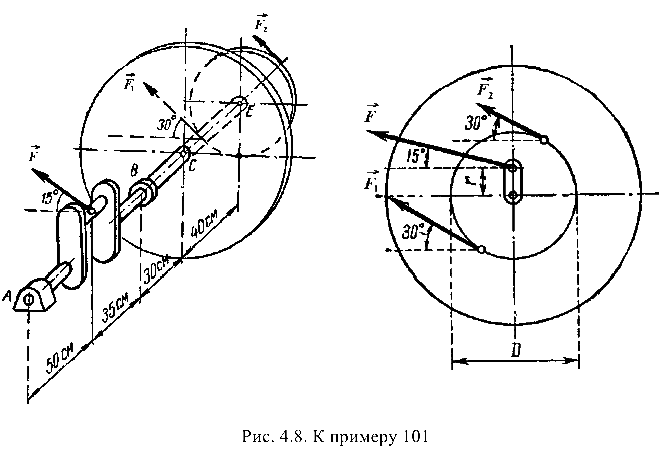
На рис. 4.8 изображен коленчатый вал двигателя. При вертикальном положении средней плоскости колена шатуна сила 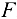 , действующая на середину шейки вала, составляет 12 кН и направлена к плоскости, перпендикулярной оси вала, под углом 15° к горизонтали. На оси вала в точке
, действующая на середину шейки вала, составляет 12 кН и направлена к плоскости, перпендикулярной оси вала, под углом 15° к горизонтали. На оси вала в точке 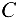 закреплен маховик весом
закреплен маховик весом 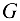 = 12 кН. В точке
= 12 кН. В точке 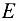 укреплен шкив диаметром
укреплен шкив диаметром 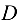 = 80 см с ремнем, передающим момент па вал рабочей машины. Ветви ремня расположены в плоскости шкива и составляют с горизонталью угол, равный 30°. Отношение натяжения ведущей и ведомой ветвей ременной передачи
= 80 см с ремнем, передающим момент па вал рабочей машины. Ветви ремня расположены в плоскости шкива и составляют с горизонталью угол, равный 30°. Отношение натяжения ведущей и ведомой ветвей ременной передачи 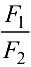 = 2. Расстояние от оси вала до оси шейки колена
= 2. Расстояние от оси вала до оси шейки колена 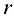 = 15 см. Расстояния вдоль оси вала показаны на рис. 4.8. Определить величины натяжения ветвей ремня
= 15 см. Расстояния вдоль оси вала показаны на рис. 4.8. Определить величины натяжения ветвей ремня 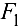 и
и 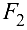 , и реакции подшипников вала
, и реакции подшипников вала 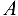 и
и 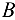 при равномерном его вращении и заданном его положении. Весом шкива и вала пренебрегаем.
при равномерном его вращении и заданном его положении. Весом шкива и вала пренебрегаем.
Решение:
Приложенные к валу силы должны удовлетворять условиям их равновесия. Прикладываем к валу заданные внешние силы: вес маховика 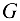 , силу давления па шейку
, силу давления па шейку 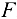 и реакции ветвей ремня
и реакции ветвей ремня 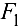 и
и 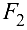 , направленные по касательной к окружности обода шкива. Отбрасывая мысленно связи, наложенные па вал в виде подшипников, заменяем их реакциями вала, разложенными па составляющие
, направленные по касательной к окружности обода шкива. Отбрасывая мысленно связи, наложенные па вал в виде подшипников, заменяем их реакциями вала, разложенными па составляющие
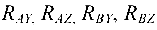
(рис. 4.9).
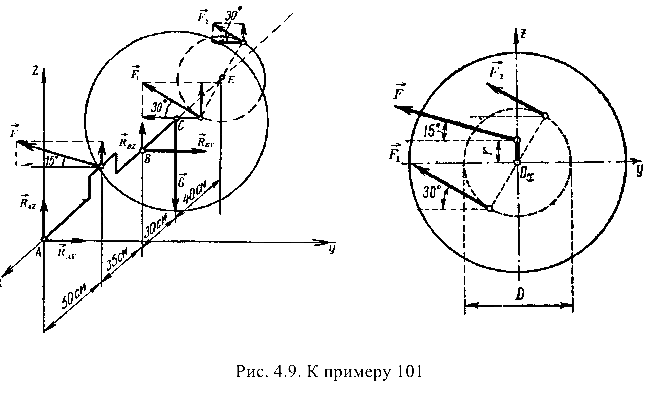
Выбрав оси координат 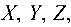 как показано на рис. 4.9, составляем уравнения равновесия системы сил, произвольно расположенных в пространстве.
как показано на рис. 4.9, составляем уравнения равновесия системы сил, произвольно расположенных в пространстве.
Составим уравнения моментов сил относительно осей координат:
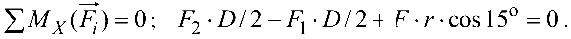
Так как
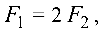
то
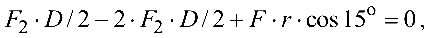
откуда
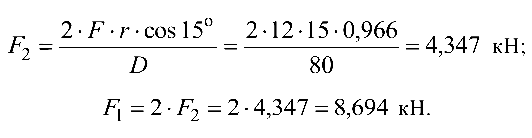
При вычислении моментов сил 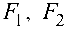 и
и 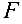 относительно оси
относительно оси 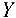 проецируем каждую из этих сил па плоскость, проходящую через точку приложения силы перпендикулярно оси
проецируем каждую из этих сил па плоскость, проходящую через точку приложения силы перпендикулярно оси 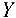 .
.
Полученные проекции
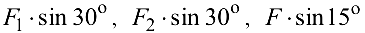
параллельны оси 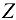 .
.
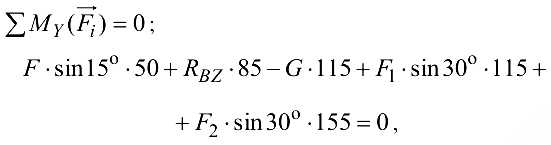
откуда
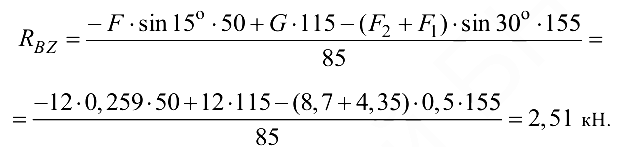
Аналогично при составлении уравнения
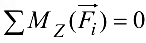
находим проекции сил 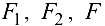 на плоскости, перпендикулярные к оси
на плоскости, перпендикулярные к оси 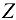 . Эти проекции параллельны оси
. Эти проекции параллельны оси 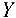 и соответственно имеют величины
и соответственно имеют величины
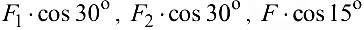
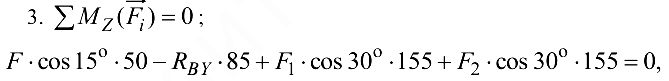
откуда
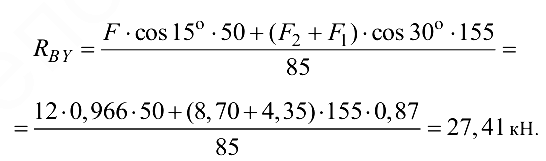
Составляем уравнения проекций сил на оси 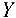 и
и 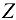 . Так как все действующие силы перпендикулярны к оси
. Так как все действующие силы перпендикулярны к оси 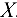 , уравнение
, уравнение 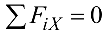 преобразуется в тождество 0 = 0.
преобразуется в тождество 0 = 0.
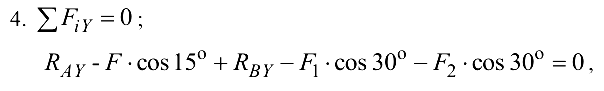
откуда
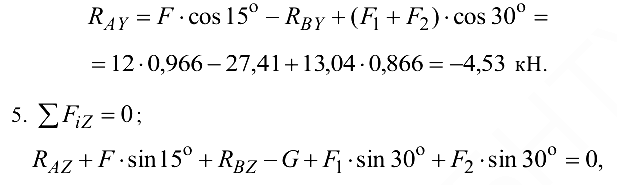
откуда определяем
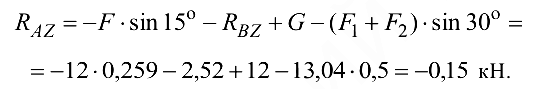
Полная реакция опоры 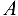
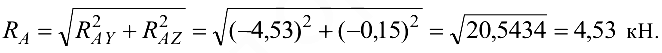
Полная реакция опоры 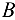
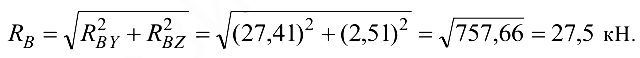
Ответ:
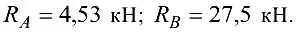
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:

