На негладкой горизонтальной плоскости лежит полушар весом и с радиусом

Задача №43.

На негладкой горизонтальной плоскости лежит полушар весом 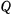и с радиусом . В точке 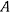на него действует горизонтальная сила 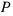. Зная значение коэффициента трения 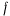между полушаром и опорной плоскостью, определить условия равновесия полушара, если расстояние 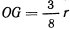(рис. 47).

Решение:

Скольжению полушара препятствует горизонтальная сила трения 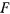, величина которой удовлетворяет неравенству 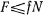, где через обозначено вертикальное давление полу-шара на плоскость. Рассматривая освобождающее вертикальное возможное перемещение полушара, легко определить из условия

Рассматривая далее поступательное горизонтальное перемещение пол у шара, будем иметь

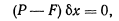
откуда следует

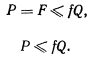
Только при выполнении этого условия возможно равновесие.

Выберем начало координат в точке контакта полушара с горизонтальной плоскостью, когда основание полушара горизонтально. Тогда горизонтальную и вертикальную координаты центра тяжести полушара и точки приложения силы 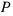можно будет представить в виде

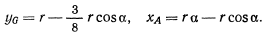
Среди возможных перемещений системы имеется поворот полушара вокруг точки контакта 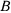. На этом перемещении будем иметь

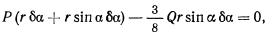
откуда находим

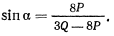
Положительное значение 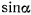получается отсюда при условии

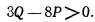
Условие существования действительного значения 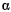имеет вид

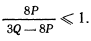
Таким образом, будем иметь

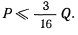
Полученные условия (1), (2), (3) являются условиями равновесия.

Задача взята со страницы подробного решения задач по всем темам теоретической механики:

Решение задач по теоретической механике

Возможно эти дополнительные задачи вам будут полезны:

Задача №42. Два одинаковых стержня и , весом и длины а каждый, могут свободно вращаться на шарнирах и . Они соединены шарнирами и с третьим стержнем, расположенным горизонтально и имеющим вес Q и длину а<>- Вся система находится в равновесии в вертикальной плоскости. Определить реакции шарниров А и С, если угол а известен (рис. 45).

Задача №43. Однородный стержень весом опирается верхним своим концом на негладкую вертикальную стенку (коэффициент трения равен ), а нижним — на гладкий горизонтальный стол и удерживается в равновесии в вертикальной плоскости при помощи привязанной к его нижнему концу и протянутой по столу веревки, которая затем перекинута через блок и несет на своем свободном конце груз весом . Найти, при каких значениях угла наклона стержня а возможно равновесие системы, а также определить реакции в точках и (рис. 46).

Задача №44. Пусть ось направлена вертикально вверх. Будем предполагать, что на материальную точку действует только сила тяжести. Проекция силы тяжести на ось будет постоянна по величине и имеет отрицательное значение —. Поэтому движение материальной точки вдоль оси будет определяться дифференциальным уравнением.

Задача №45. Материальная точка массы притягивается неподвижным центром с силой , где — постоянный коэффициент пропорциональности, — расстояние точки от . В начальный момент расстояние , а скорость образует с направлением угол . Найти уравнения движения точки и ее траекторию, принимая прямую за ось .