Задача 1.119.
На молочном комбинате для производства двух видов сливочного мороженого и двух видов пломбира требуется молоко натуральное, молоко сухое, молоко сухое обезжиренное, масло сливочное, сахар, молоко сгущенное, молоко сгущенное обезжиренное, а также используется соответствующее оборудование для расфасовки и упаковки мороженого. Нормы затрат указанных ресурсов на производство 1 т мороженого приведены в табл. 1.57.
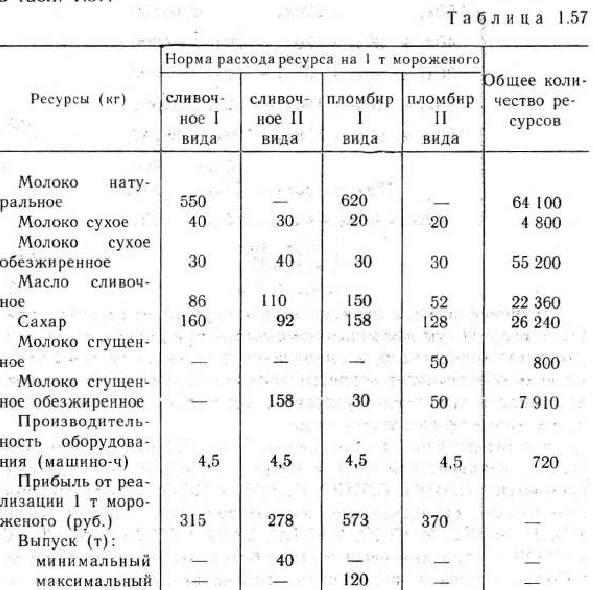
В этой же таблице указана прибыль от реализации 1 т мороженого каждого вида, приведено общее количество ресурсов данного вида, имеющееся в распоряжении молочного комбината, а также указаны минимально возможный выпуск сливочного мороженого II вида и максимально возможный — пломбира I вида (эти границы определены на основе установившегося спроса на мороженое).
Определить план производства мороженого молочным комбинатом, обеспечивающий максимальную прибыль от его реализации. Используя ППП ЛП АСУ, найти решение задачи и провести послеоптимизационный анализ найденного решения.
Решение:
Составим математическую модель задачи. Для этого будем считать, что сливочного мороженого I и II видов будет изготовлено соответственно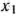 
и 
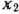тонн, а пломбира I и II видов — 
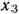и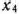 
тонн. Тогда математическая постановка задачи состоит в определении максимального значения функции
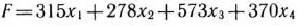
при условиях
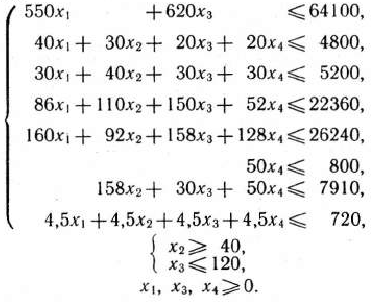
Значение целевой функции задачи определяет величину прибыли, получаемую молочным комбинатом при данном плане производства мороженого, а выполнение неравенств системы ограничений обеспечивает непревышение имеющихся ресурсов каждого вида и выполнение условий относительно возможного выпуска мороженого данного вида.
В соответствии с требованиями ППП ЛП АСУ переменным задачи, неравенствам (93) и целевой функции (92) присваиваем имена: СЛИВ1, СЛИВ2, ПЛОМ1 и ПЛОМ2 — столбцовые переменные, обозначающие имя мороженого данного вида; МОЛН, МОЛС, МОЛСО, МАСЛО, САХАР. МОЛСГ, МОЛСГО и ОБОР — строчные переменные, обозначающие имя ресурсов; ПРИБ — строчная переменная, обозначающая имя целевой функции. Тогда имеем
Используя последнюю систему уравнений, составляем матрицу исходных данных задачи (табл. 1.58).
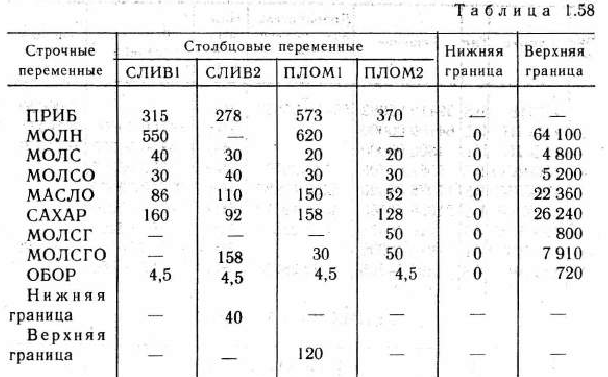
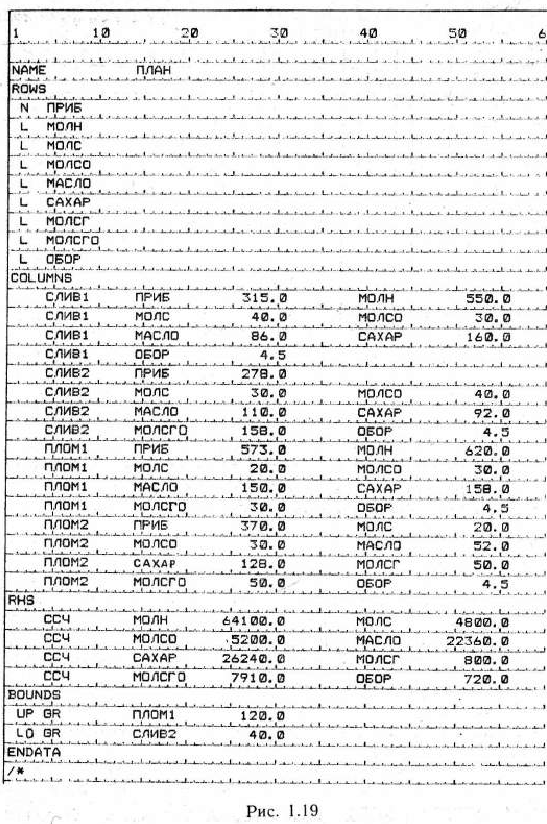
Используя табл. 1.58, исходные данные задачи записываем на бланке для их последующей перфорации (рис. 1.19).
Следующим шагом является построение управляющей программы решения данной задачи. Эта программа приведена на рис. 1.20 н, как видно из этого рисунка, отличается от программы решения задачи линейного программирования (см. рис. 1.13) тем, что последняя содержит оператор RANGE, включение которого необходимо для получения отчета о послеоптимизационном анализе решения задачи.
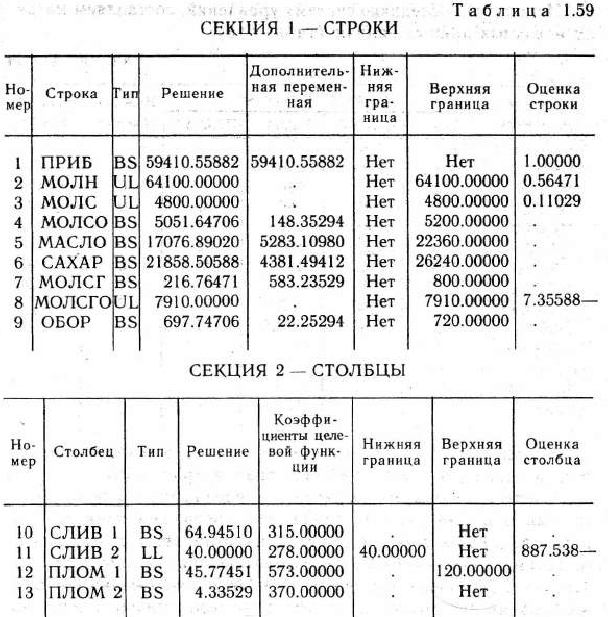
После этого производим решение задачи на ЭВМ. Результаты решения приведены в табл. 1.59 и 1.60.
Приведенный в табл. 1.59 отчет о решении задачи состоит из двух частей: СЕКЦИИ 1 — СТРОКИ, в которой содержится информация о строчных переменных, а СЕКЦИИ 2 — СТОЛБЦЫ, содержащей информацию о столбцовых переменных. Структура этих отчетов подробно рассмотрена в § 1.5.
Из табл. 1.59 следует, что оптимальным планом производства мороженого молочным комбинатом является такой план, согласно которому будет изготовлено сливочного мороженого I и II видов соответственно 64,945 и 40,0 т, а пломбира I и II видов — 45,774 и 4,335 т. При этом общая прибыль молочного комбината от реализации указанного количества мороженого составляет 59410,127 руб. Отметим, что несовпадение величины прибыли, приведенной в табл. 1.59, определяется округлением полученных значений переменных. Это округление с точностью до тысячных
мы будем использовать и при проведении послеоптимизационного анализа решения задачи.
Отчет о послеоптимизационном анализе решения задачи характеризуется информацией, содержащейся в табл. 1.60, которая включает четыре части: СЕКЦИЯ 1 — СТРОКИ НА ГРАНИЦЕ, СЕКЦИЯ 2 — СТОЛБЦЫ НА ГРАНИЦЕ, СЕКЦИЯ 3 — СТРОКИ НА ПРОМЕЖУТОЧНОМ УРОВНЕ и СЕКЦИЯ 4 — СТОЛБЦЫ НА ПРОМЕЖУТОЧНОМ УРОВНЕ. Структура этого отчета аналогична структуре отчета о послеоптимизационном анализе решения задачи, получаемом с использованием ППП ЛП2. Вместе с тем в отчете о послеоптимизационном анализе решения задачи, получаемом с использованием ППП ЛП АСУ, имеется дополнительный столбец «Ввод—вывод из базиса», содержащий имя переменной, которая определяет вектор, меняющий свое состояние (выйдет из базиса или войдет в базис), если значение анализируемой переменной выйдет за допустимые
пределы. При этом в последней графе табл. 1.60 указывается, на какой уровень перейдет переменная, если определяемый ею вектор будет введен или выведен из базиса.
С учетом сказанного выше проведен послеоптимизационный анализ полученного решения нашей задачи. Рассмотрим, например, вторую строку секции 1. Данные этой строки характеризуют использование сухого молока. В третьей графе этой строки ука-
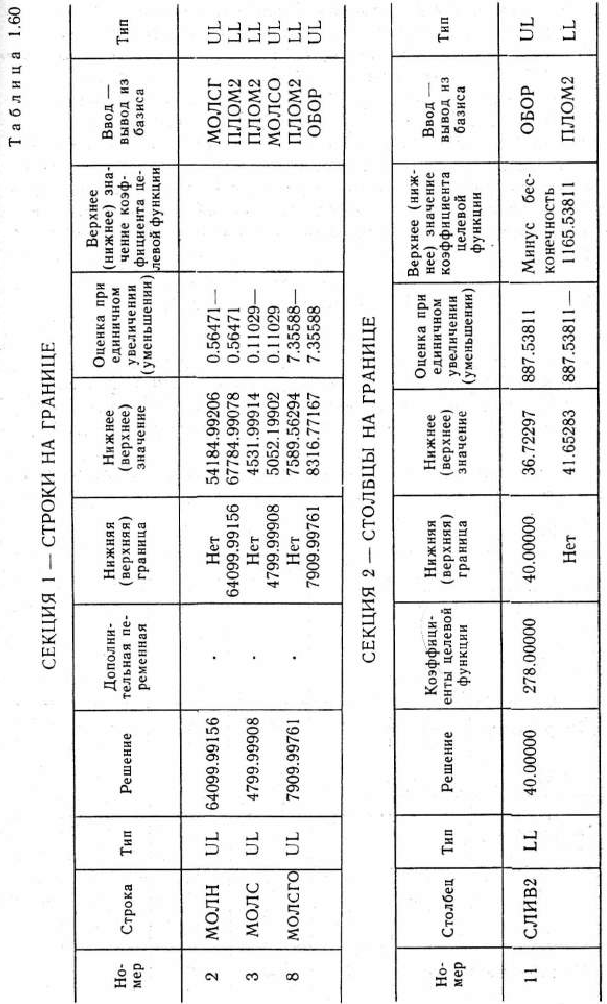
зан тип переменной UL, т. е. оговорено, что она приняла свое верхнее предельное значение. В последующей четвертой графе указано это значение, а из пятой графы видно, что количество неиспользованного сухого молока при оптимальном плане производства мороженого равно нулю. Из следующей графы видно, что нижняя граница использования сухого молока не определена (в табл. 1.60 это отмечено словом «Нет», а верхняя граница равна 4799,999 т). Данное число совпадает со значением переменной МОЛС в решении задачи, поскольку эта переменная приняла значение на споей верхней границе. Если верхняя граница будет увеличиваться, то базис, определяющий исходный оптимальный план, будет оставаться без изменения до тех пор, пока значение переменной не достигнет верхнего значения, равного 5052,199 т. Аналогично, уменьшение нижней границы переменной МОЛС без изменения базиса, определяющего оптимальный план, возможно до нижнего значения, равного 4531,999 т. Мри дальнейшем изменении нижней или верхней границы переменной МОЛС произойдет изменение базиса за счет «Ввода—вывода из базиса» вектора, определяемого переменной, стоящей в предпоследней графе табл. 1.60, а именно переменной ПЛОМ2 или МОЛСО. При этом переменная ПЛОМ2 перейдет на уровень LL, а переменная МОЛСО — на уровень UL.
Далее, увеличение количества сухого молока на 1 кг, т. е. увеличение значения переменной МОЛС на единицу, приведет к увелнченню значения целевой функции, т. е. прибыли от реализации мороженого, на 0,11 руб. Точно так же уменьшение значения переменной МОЛС на единицу приведет к уменьшению значения целевой функции на 0,11 ед. Это справедливо при изменении переменной МОЛС от 4531,999 до 5052,199.
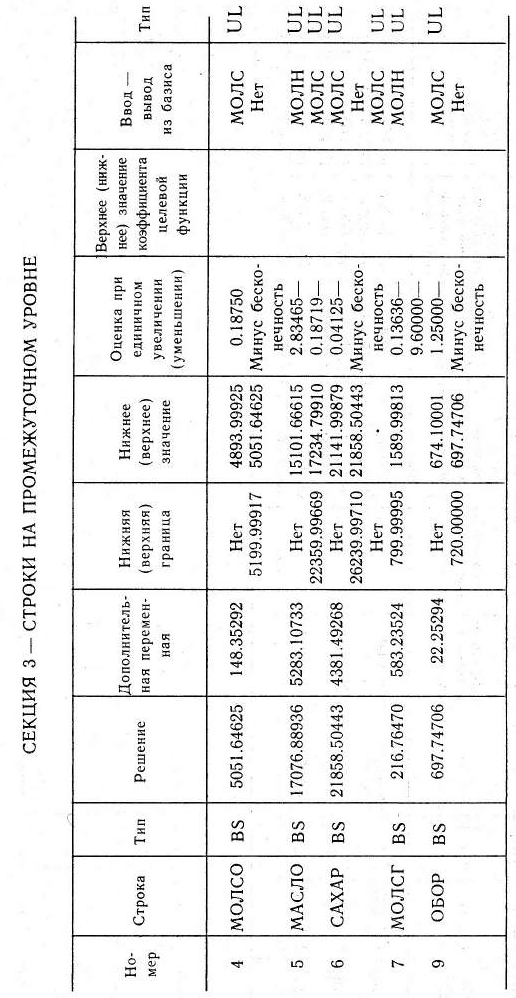
Аналогично можно провести анализ использования и других ресурсов, которые полностью или частично необходимы для реализации оптимального плана изготовления мороженого, т. е. аналогично можно провести анализ строк СЕКЦИИ 3 табл. 1.60.
Остановимся теперь на послеоптимизационном анализе производства продукции. Рассмотрим, например, анализ переменной ПЛОМ1, т.е. рассмотрим 12-й столбец, находящийся в СЕКЦИИ 4 табл. 1.60. Из этого столбца видно, что переменная Г1ЛОМ1 приняла свое промежуточное значение (тип BS) винтер-вале ее изменения от 0 до 119,999. Это значение равно 45,774, т. е. оптимальным является выпуск 45,774 т пломбира I вида, цена 1 т которого равна 573,000 руб. Если в принудительном порядке увеличить производство пломбира I вида на 1 т, то это приведет к уменьшению общей прибыли молочного комбината от реализации мороженого на 4,090 руб. Каждое уменьшение в принудительном порядке производства пломбира I вида на 1 т приводит к уменьшению прибыли молочного комбината на 283,0 руб. Таким образом, всякое принудительное изменение значения переменной ПЛОМ1 относительно значения, принятого в оптимальном плане производства продукции, приводит к уменьшению значения целевой функции. Это изменение значения целевой функции является более существенным при уменьшении производства пломбира I вида на 1 т, чем при увеличении его производства на 1 т. При этом указанные изменения целевой функции задачи имеют место до тех пор, пока выпуск пломбира I вида не будет увеличен до 52,999 т или уменьшен до 26.333 т. Если производство пломбира I вида не будет заключено в указанных границах, то нарушатся как указанные оценки изменения значения целевой функции, так и структура оптимального плана.
Далее, оптимальный план производства мороженого не изменится до тех пор, пока цена 1 т пломбира I вида не станет меньше 285,0 руб. и не больше 577,091 руб. Иными словами, если цена 1 т пломбира I вида будет выше 577,091 руб., то оптимальным станет его изготовление в количестве 52,999 т. Если же цена 1 т пломбира станет меньше чем 285,0 руб., то оптимальная величина его производства будет равна 26,333 т.
Из изложенного выше видно, что использование ППГ1 ЛП АСУ позволяет довольно полно проводить послеоптимизацион-ный анализ полученного решения задачи линейного программирования. Это очень важно для практики принятия управленческих решений, поскольку для каждой конкретной ситуации позволяет принять наиболее приемлемое управленческое решение.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
