Задача 1.118.
На мебельной фабрике изготовляется пять видов продукции: столы, шкафы, диваны-кровати, кресла-кровати и тахты. Нормы затрат труда, а также древесины и ткани на производство единицы продукции данного вида приведены в табл. 1.53.
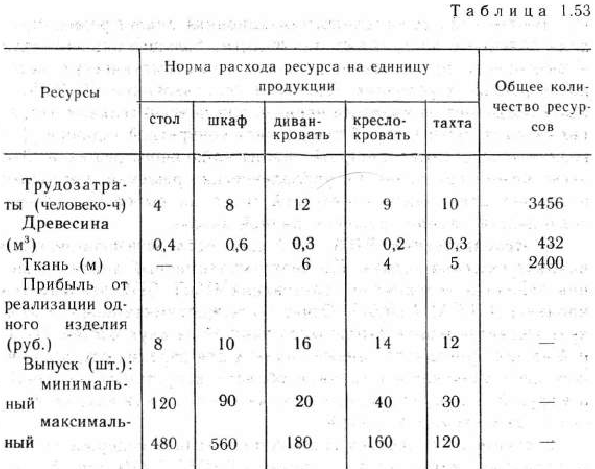
В этой же таблице указана прибыль от реализации одного изделия каждого вида, приведено общее количество ресурсов данного вида, имеющееся в распоряжении фабрики, а также указано (на основе изучения спроса), в пределах каких объемов может изготовляться каждый вид продукции.
Определить план производства продукции мебельной фабрикой, согласно которому прибыль от се реализации является максимальной. Используя ППП Л112, найти решение задачи, а также провести послеоптимизационный анализ полученного решения.
Решение:
Составим математическую модель задачи. Для этого предположим, что мебельная фабрика изготовит каждый из пяти видов продукции (стол, шкаф, диван-кровать, кресло-кровать и тахту) в количестве, соответственно равном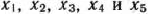 
ед. Тогда математическая постановка задачи состоит в определении максимального значения функции
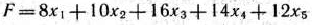
при условиях
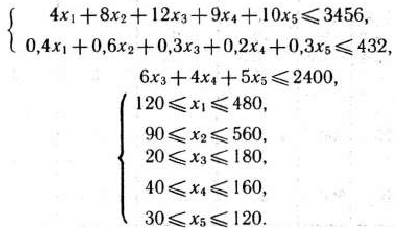
Значение целевой функции задачи (89) определяет величину прибыли, получаемую мебельной фабрикой при данном плане производства продукции, а выполнение неравенств (90) системы ограничений обеспечивает непревышение имеющихся в распоряжении фабрики ресурсов.
В соответствии с требованиями ППП ЛП2 каждой переменной, каждому неравенству системы ограничений (90) и целевой функции (89) присваиваем имена. Переменным 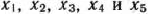присвоим соответственно имена СТОЛ, ШКАФ, ДИВАН, КРЕСЛО и ТАХТА. Первому неравенству системы ограничений (90) дадим имя ТРУД, второму — ДРЕВ, третьему — ТКАНЬ, а целевой функции — ПРИБ. С учетом введенных обозначений целевую функцию и систему ограничений задачи записываем в виде системы уравнений:
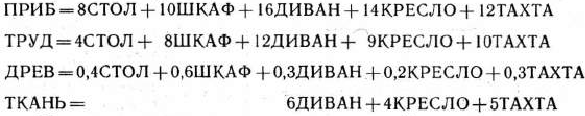
Используя последнюю систему уравнений, составляем матрицу исходных данных задачи (табл. 1.54).
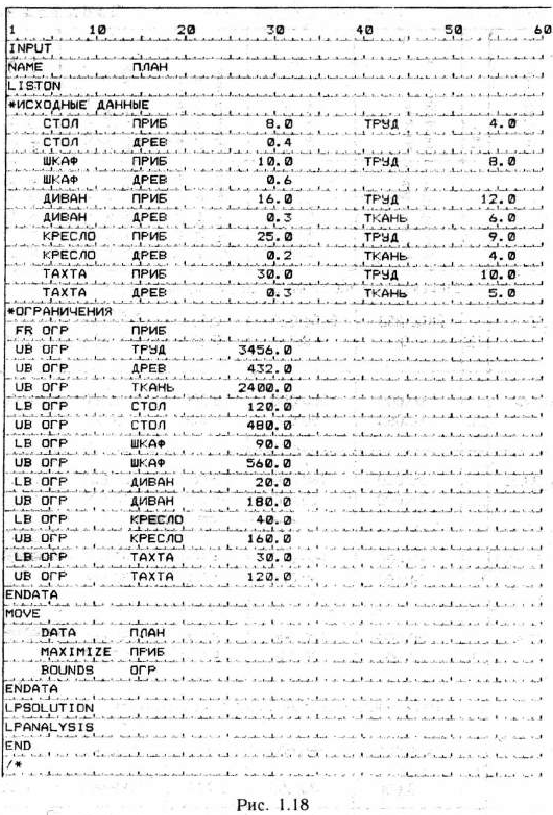
Исходные данные задачи, операторы управления и операторы описания записываем на специальном бланке (рис. 1.18), так же как мы это делали при нахождении решения задачи линейного программирования в § 1.5. Вместе с тем, чтобы получить отчет о послеоптнмизационном анализе решения задачи, после оператора LPSOLUTJON указываем оператор LPANALYSIS (ср. рис. 1.10 и 1.18).
После этого производим решение задачи на ЭВМ, Результаты решения выдаются в виде двух таблиц (см, табл. 1.55 и 1.56),
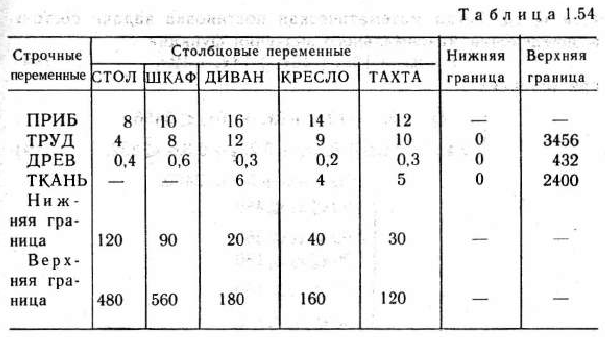
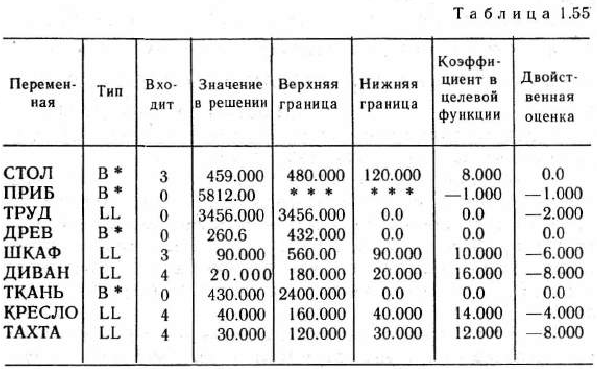
В табл. 1.55 содержится отчет о решении задачи (о чем было подробно сказано в § 1.5), а в табл. 1.56 — отчет о послеоптимиза-ционном анализе решения задачи.
Из табл. 1.55 видно, что оптимальным планом производства продукции мебельной фабрикой является план, согласно которому изготовляется 459 столов, 90 шкафов, 20 диванов-кроватей, 40 кресел-кроватей и тахты в количестве, равном 30. В соответствии с этим планом производства продукции прибыль фабрики от ее реализации является максимальной и равна 5812 руб., причем полностью используются трудовые ресурсы и остаются не использованными древесина и ткань.
Проведем теперь анализ полученного решения задачи. Для этого воспользуемся данными та-бл. 1.56. Как видно, эта таблица состоит из двух частей. В первой части приводятся данные для анализа переменных, принявших свои значения на границе области их допустимых значений (переменные типа LL, UL и FQ), а во второй части — для переменных, принявших свои значения внутри области допустимых значений (переменные типа В*).
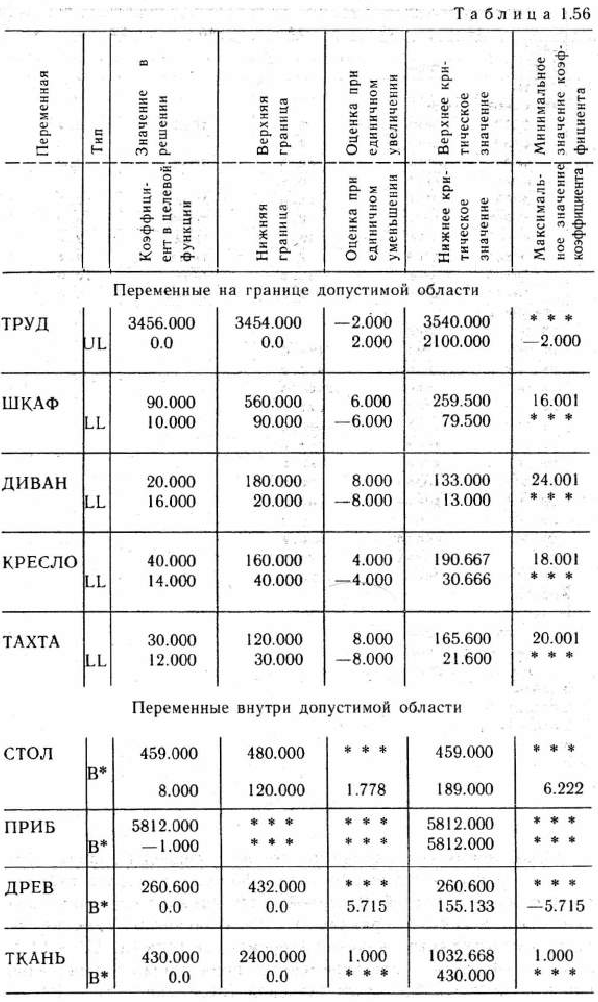
Первые четыре графы табл. 1.56 повторяют исходные данные и воспроизводят результат решения задачи.
В пятой графе указываются оценки, характеризующие степень изменения целевой функции при единичном изменении значения данной переменной (заметим, что знаки оценок соответствуют тому случаю, когда находится минимум целевой функции; в случае максимизации целевой функции, как в рассматриваемой задаче, знаки оценок следует изменить на противоположные). Действие оценок справедливо в интервале от нижнего до верхнего предельного значения переменной. Так, например, если принудительно увеличить выпуск диваиов-кроватей на один и довести до 21 (оптимальным планом производства продукции предусмотрено изготовление 20 диванов-кроватей), то это приведет к уменьшению прибыли мебельной фабрики на € руб.
Такое изменение прибыли будет иметь место при каждом увеличении выпуска на один диван-кровать до тех пор, пока выпуск данной продукции не превзойдет 133 шт.
Далее, если теперь рассмотрим один из видов ресурсов, например древесину, то видим, что этот вид ресурсов при оптимальном плане производства продукции используется не полностью. Вместе с тем если считать, что его объемы заключены между 260,6 и 155,133 м3, то каждое принудительное уменьшение объема использования данного ресурса на 1 м’1 приведет к уменьшению прибыли на 5,715 руб.
Рассмотрим теперь шестую графу табл. 1.56. В ней указываются пределы, в которых принудительно можно изменять значения переменных, так что базис, определяющий данный оптимальный план, остается неизменным. Так, например, если изготовле-. ние столов, выпуск которых в соответствии с оптимальным планом равен 459, изменять от 189 до 459, то базис, определяющий исходный оптимальный план, не меняется. Этот базис сохраняется и в том случае, если объем трудозатрат изменяется в пределах от 2100 до 3540 человеко-ч.
Рассмотрим, наконец, седьмую графу табл. 1.56. В ней указывается, в каких пределах могут изменяться значения коэффициентов целевой функции задачи, так что найденный оптимальный план остается неизменным. При этом в указанной графе табл. 1.56 приведены данные для того случая, когда находится минимум функции. В том случае, когда находится максимум функции (как в рассматриваемой задаче), в шестой графе верхние и нижние строки следует поменять местами. Так, например, для диванов-кроватей, прибыль от реализации которых равна 20 руб., максимальное значение коэффициента при переменной ДИВАН в целевой функции равно 24, а минимальное не ограничено. Это означает, что если прибыль от реализации одного дивана-кровати не превышает 24 руб., то выпускать диваны-кровати сверх установленного задания (20 шт.) невыгодно. Если прибыль окажется больше чем 24 руб., то выпуск диванов-кроватей при оптимальном плане производства продукции превысит 20 шт.
Из рассмотренного примера видно, что использование ППП ЛП2 позволяет не только найти решение задачи, но и провести довольно полный послеоптимизационный анализ полученного решения. Еще более полный послеоптимизационный анализ позволяет провести использование ППП ЛП АСУ.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
