Оглавление:
Задача №1.2.11.
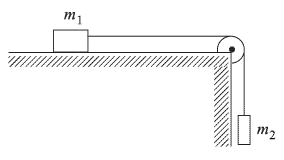
На горизонтальном столе находится брусок массы 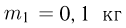 , которому привязана нерастяжимая нить. Второй конец нити перекинут через блок и прикреплен к грузу массы
, которому привязана нерастяжимая нить. Второй конец нити перекинут через блок и прикреплен к грузу массы 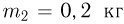 . Коэффициент трения между бруском и столом
. Коэффициент трения между бруском и столом 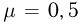 . Пренебрегая массой блока, определить силу
. Пренебрегая массой блока, определить силу 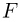 , с которой нить действует на блок.
, с которой нить действует на блок.
Решение:
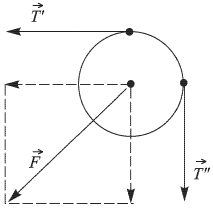
Натянутая нить взаимодействует с блоком во всех точках их соприкосновения. При этом полная сила 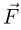 , с которой нить действует на блок, равна векторной сумме сил натяжения
, с которой нить действует на блок, равна векторной сумме сил натяжения 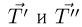 , приложенных в точках схода нити с блока (см. рисунок).
, приложенных в точках схода нити с блока (см. рисунок).
Из невесомости нити и блока следует, что натяжение нити во всех точка одинаково: 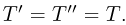 Следовательно, величина силы, с которой нить действует на блок, определится из равенства:
Следовательно, величина силы, с которой нить действует на блок, определится из равенства:
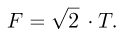
Для того, чтобы найти натяжение нити, воспользуемся законами Ньютона. Решая задачу в общем виде, необходимо иметь в виду, что предоставленная самой себе система придет в движение только в том случае, если коэффициент трения между грузом 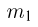 и столом достаточно мал. Предположив это, запишем уравнения движения грузов под действием приложенных к ним сил:
и столом достаточно мал. Предположив это, запишем уравнения движения грузов под действием приложенных к ним сил:
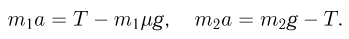
Здесь 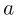 — величина ускорения в системе, одинаковая для обоих грузов в силу нерастяжимости нити. Найденное из этой системы натяжение нити равно:
— величина ускорения в системе, одинаковая для обоих грузов в силу нерастяжимости нити. Найденное из этой системы натяжение нити равно:
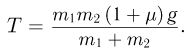
Если трение между грузом 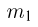 и столом велико, система будет находиться в покое. В этом случае
и столом велико, система будет находиться в покое. В этом случае
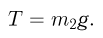
Значение коэффициента трения, при котором предоставленные самим себе грузы будут покоиться, определяется из условия:
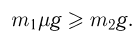
Таким образом, ответ к задаче должен быть сформулирован в следующем виде: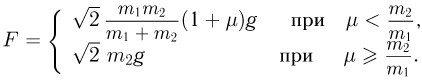
При конкретных данных задачи 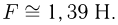
Эти задачи взяты со страницы решения задач по физической механике:
Решение задач по физической механике
Возможно эти задачи вам будут полезны:

