n-ые производные некоторых функций

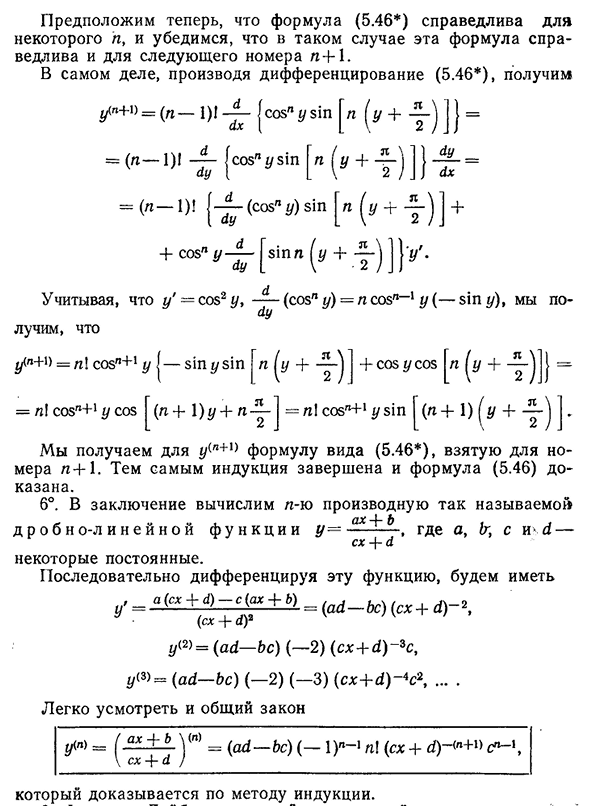
n-ые производные некоторых функций

• N-я производная некоторых функций. 1°. Вычислить производную n-го порядка степенной функции y=x®(x>0,и-любое вещественное число). В последовательной производной y’=Aha~1, y(2)=a(a-1) x~2,y(3)=a(a-1) (a-2) ha_3,… . Поэтому легко понять общий закон (xТ.

Итак, N-я производная полинома T-го порядка от n>t равна.Ноль. [LP(x) 4-+In C(x)]n=Li(x) 4-In (n) (x), где L и B-константы.§6. Пользовательские производные и дифференциальные высшего 215 2°. Если вы делаете последовательное дифференцирование, вы получаете y/=a x1ph, y^ — Ah1x2x, y (3)=a1p3a……

Общая формула, которая легко устанавливается методом индукции, имеет следующий вид (АГ) (га)=Ah1PP собой. Людмила Фирмаль

Особенно, 3°. Вычислите производную n-го порядка функции y=81PX. Первая производная этой функции может быть записан как y’=Соз х=51p позволяют вести съемку быстро. Таким образом, производная функции y=81px добавляет значение аргумента этой функции. Таким образом, мы получаем формулу .Два. ___________________ (81ph) < ha)=8SH+ • 4°. Очень похожим образом устанавливается формула (Соз х) (р)=Соз 5°. Если вычислить N-ю производную функции g / =agc1§X, то математическая индукция докажет, что справедлива следующая

формула: (agc1§x)(«) = (1(^ ~ y/2 5{p p(a g C1§x+y^. (5.46) G / =ags1§x, x = 1§y,———= ———— = SO2//, мы можем переписать установленное выражение как 1+x2 1+1E2y, =(C-1 / / SOP u31P Проверим эффективность формулы (5.46) по индукции. В N=1, благодаря пункту 3§5, y’=(AGS!§х)’=-!- =CO2y. то же самое уравнение 1+x2 может быть получено при n=1of (5.46), если достаточно Рассмотрим, что 51P[y+ — y^=C O5 1/). Итак, для n=1 справедлива формула (5.46).216Ч. 5. Предположим, что дифференциальная формула (5.46) действительна для некоторого n, и в этом случае убедитесь, что эта формула

• действительна для следующего числа n+1: Фактически, производя производную (5.46), получаем— 1 |1 / so8p y81P=(P-1) 1 1 1so5p y31P Yu I=(I-1)! Я—(SO8P u)81P I Lu Если Y ‘ =CO82y,— — — (S03p y)=p S08p-1y (- ZT y)、- г(п+’)=н\S05p+1У|-81pu81•Н Г н//г+,—»= 008″+ ‘ у поп(П+1)п+п -^ — [«(‘+- год

) ] ) “ Пи! Sozp+ ‘ u81P|(p+1) (u+-u -). Получаем формулу вида, принятого для числа n+1 (5.46), для y (n+1). Таким образом, индукция завершена, и Формула (5.46) доказана. 6°. В заключение вычислим N-ю производную от так называемого «Ah — \ — B». д р О Б и о-л и Н Е Н О й ф у Н К И Й= ——— , где A, C, A-CX+4

Некоторые из них являются постоянными. Последовательно различая эту особенность、 ,=А^+^- Людмила Фирмаль

С^+Б)=a_BS}+^2> (CX+4) 2 и<2)=(AI.- БС) (-2) (СХ+й)-3С, г<3>=(АИ-БС) (-2)(-3)(СХ+й) — конфигурацию 4s2…….. Легко увидеть и общий закон u(A^ — & C) (-1) «-1P1(CX+f_ (p+1)s » -1,\CX+4 / Это доказывается методом индукции.

Смотрите также:

Методическое пособие по математическому анализу

Понятие компактности множества	Умножение неквадратных функциональных матриц
Понятие производной n-го порядка	Определение производной