Оглавление:
Возможно, особое свойство рассуждений — это способность достигать конкретной цели, то есть находить необходимый вариант среди других, которые в принципе приемлемы, но не приводят к желаемому результату. Например, если у обезьяны в клетке есть куча различных предметов, но она может получить банан, только выбрав из этой кучи коробку, на которую можно встать, и палку, которой можно сбить банан, то мы судим об интеллекте обезьяны по тому, как она справляется с выбором.
Приемлемыми вариантами являются комбинации некоторых элементов: Действия в практических делах, выводы в доказательствах, цвета и звуки в искусстве. Может ли быть так, что для получения искомой комбинации нужно просто перебирать варианты один за другим и отбрасывать все неподходящие?
Бесполезность такого подхода вытекает из простого факта, известного в кибернетике как комбинаторный взрыв. Дело в том, что если элементы можно свободно группировать вместе, то общее множество комбинаций (по мере увеличения числа элементов в множестве) растет чрезвычайно быстро, экспоненциально. Таким образом, имея алфавит всего из десяти знаков, можно составить 10100 текстов длиной в сто букв!
Машине, которая могла бы перебирать даже миллиард таких стобуквенных слов в секунду (что, конечно, является фантастической скоростью), понадобилось бы для этого около 1074 лет. Для сравнения: время с момента космологического большого взрыва составляет «всего» 1010 лет. Поэтому проверить все варианты невозможно ни для «медленного» человеческого разума, ни для компьютера, каким бы совершенным он ни был.
И все же каким-то образом появляются уникальные тексты со многими сотнями и тысячами знаков (в музыке Моцарта ни одна нота не может быть тронута). В поиске таких новых и незаменимых сочетаний и заключается суть творчества. «Но где-то он есть, тот — единственный, необъяснимый, тот — гениальный порядок звучащих нот, гениальный порядок обычных слов!». (Р. Рождественский).
Поэтому должны существовать способы найти «иголку» необходимого, не копаясь в «стоге сена» возможного. Концепция Л.И.Верховского позволяет определить подходы к формализации такого процесса.
Понятно, что построение желаемой комбинации было бы невозможно, если бы оно начиналось сразу на уровне тех элементов, в которых она в конечном итоге будет выражена — назовем этот уровень языком реализации. Ведь недостаточно знать буквы, чтобы написать роман, и правила дорожного движения, чтобы найти нужный адрес.
Поэтому мы всегда используем не один язык, а их целый набор. С помощью этого набора мы пытаемся решить проблему в целом, то есть свести ее к ряду подпроблем, эти подпроблемы — к еще более мелким, и так далее, пока каждая из них не станет достаточно простой, чтобы быть выраженной на языке реализации. По сути, мы постепенно разлагаем сложную проблему на все большее количество более простых и простых проблем. Это как если бы мы использовали набор карт разного масштаба для планирования маршрута.
На самом деле, при определении пути мы начинаем с самой грубой карты, которая покрывает весь маршрут. От этого мы переходим к небольшому набору более подробных карт, а от каждой из них — к нескольким еще более подробным. И каждый раз мы легко находим то, что нам нужно, потому что каждая обзорная карта имеет значение, которое резко ограничивает дальнейший поиск. Таким образом, иерархия языков содержит противоядие от комбинаторного взрыва.
Очевидно, что успех всего многоуровневого процесса зависит от того, насколько полным является имеющийся набор «карт», не пропущены ли целые уровни или отдельные экземпляры. Однако такая полнота возможна только в хорошо изученной области. Именно недостаток знаний является наиболее характерным и требует усилий по расширению и реорганизации лингвистических инструментов.
Чтобы понять эволюцию таких инструментов, удобно обратиться к языкам программирования.
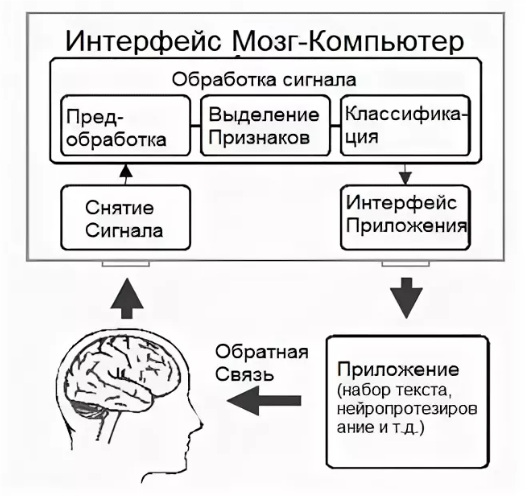
Программисткие технологии
Схема обычного современного компьютера содержит машинный язык инструкций, состоящий из простых арифметических и логических операций. Примитивность этого языка — цена универсальности: предполагается, что машина может использоваться для различных целей, и самые сложные дома можно построить из маленьких кирпичей, чего нельзя сказать о больших бках.
Однако каждый конкретный пользователь решает только свой узкий круг проблем, и универсальность ему не нужна. Напротив, он хотел бы вращать большие блоки, что позволило бы ему уменьшить проскакивание. Другими словами, ему нужен язык, ориентированный именно на его проблемы. Так как же его получить?
При написании самых простых программ некоторые комбинации команд постоянно повторяются, они как бы слипаются. Такой комбинации можно дать имя, ввести ее в память, и оператор языка более высокого уровня готов. (Это похоже на выработку условного рефлекса — повторяющиеся стимулы и реакции становятся единым целым). Этот вариант действий можно назвать способом «снизу вверх».
Но есть и другой путь — «сверху». Анализируется множество всех задач, которые необходимо решить, и производится поиск набора наибольших возможных частей, которые составят необходимый алгоритм. Снова проводя параллель со строительством, можно сказать, что они определяют набор блоков, из которых можно будет построить все здания заданного типа.
Здесь человек использует свое преимущество перед машиной в разнообразии своих представлений о мире. Для компьютера этот язык больших блоков совершенно непонятен, и он должен перевести каждый блок в набор строительных блоков — машинных инструкций. Для этого собирается программа-транслятор (опять же, с помощью иерархического разбиения). В разных случаях будут разные наборы блоков; таким образом, возникают сотни алгоритмических языков — каждый из них по-своему разделяет мир.
В этих отношениях проявляется общий принцип рассуждения — работа на вершине языковой иерархии. Если у нас нет в наличии языка высокого уровня, его необходимо создать. Главная цель здесь — избежать множества вариантов.
Конечный результат, например, обоснование утверждения, должен быть сведен к чему-то легко понимаемому: Аксиомы в формальной теории, атомные и молекулярные представления в химии (это язык реализации). Поэтому задача состоит в том, чтобы спуститься на этот уровень, а затем в обратном направлении (снизу вверх) сделать логический вывод, строгую дедукцию.
Две логики
Еще в школе, на уроках геометрии, мы хорошо усваиваем суть строгой логической системы: если удается провести цепочку умозаключений от исходных постулатов до искомого утверждения, то сомнений в его истинности нет (пока кто-то, как Лобачевский, не усомнится в основаниях). Но если цепочка умозаключений достаточно длинная, то если вы знаете только аксиомы, вы не сможете построить доказательство без большого перечисления.
Таким образом, снова необходимы целые блоки вычетов. Для этого мы сначала решаем очень простые задачи (цепочки короткие), а каждую уже решенную запоминаем — они становятся понятиями более высокого уровня (это то, что мы называем путь «снизу»). Наиболее важные из них, т.е. отражающие общие свойства всего множества задач, называются теоремами.
Теперь, сталкиваясь с более сложной проблемой, не нужно сводить ее к постулатам, а просто представить ее как комбинацию уже известных проблем и доказанных теорем (путь вниз от них уже пройден). Решение проблемы — это «как выкладывание пола в комнате паркетом, выкладывание проблемы аксиомами». Нахождение этой схемы отражает построение доказательства, то есть состав и порядок выводов. Понятно, что если проблема достаточно велика, то решить ее сразу невозможно (тот самый большой перебор). Поэтому сначала необходимо расширить набор правильных утверждений. Давайте решать более простые задачи. Давайте просто наполним их аксиомами. Имея в виду эти блоки, мы можем теперь вернуться к сложной проблеме. Понятно, что она будет сведена к тому, что уже решено.
Именно так строится обучение по учебнику или у хорошего учителя, когда специально подобранная серия все более трудных заданий позволяет постепенно наращивать знания ученика. Но что делать в новой, неизведанной местности?
Если есть какие-то установленные факты, то все начинается с них. Внимательно изучите их структуру и попытайтесь найти скрытую закономерность, некий общий принцип. Мы выявляем похожие контуры и мотивы — определяем для себя эвристику, которая значительно ограничивает количество приемлемых гипотез. Затем мы просеиваем все правдоподобные варианты.
Наконец, после долгих раздумий и безуспешных попыток, мы находим — Эврика! — Все факты представлены как комбинации нескольких гипотез. Мы переживаем тот редкий и незабываемый момент, который называется озарением.
Понятно, что введение гипотез элементов — это привычный путь «сверху». Загвоздка в том, что сами эти элементы могут оказаться слишком большими, слишком далекими от обычных представлений, чтобы их можно было сразу выразить на языке обыденного знания. Часто это лишь смутные ощущения, когда автор догадки уже уверен в ее правильности, но еще не может убедить в этом других. Как говорил Карл Гаусс: «… Я знаю свои результаты, я просто не знаю, как я их получу».
И все же, несмотря на образовавшуюся логическую брешь, появление таких неясных образов — важный этап. Это соответствует интуитивному решению, постановке новых целей, которые определяют все последующее, то есть формулировке и обоснованию гипотезы, а затем ее превращению в теорию. Любая интуитивная картина — «замок в облаках» — должна быть закреплена (путем дальнейшего подразделения) на твердой почве аксиом и теорем. Очевидно, что интуиция — это не что-то мистическое, а результат движения мысли «вширь», культивирующей свой особый взгляд, который упрощает общую картину.
Таким образом, существует два основных этапа формирования теорий: сначала угадывание языка на самом высоком уровне для описания имеющихся фактов, а затем строгое обоснование.
Как исчислять идеи
Великий Х. Лейбниц в свое время выдвинул программу «универсальной характеристики» — языка, символы которого отражали бы свое значение, то есть отношения к другим понятиям — «их знаки сочетались бы в соответствии с порядком и связью вещей». Все размышления, по его мнению, должны сводиться к вычислению на этом языке по определенным правилам. Пока что этот проект преуспел лишь наполовину, в формализации дедуктивного вывода (компьютер делает то же самое); но логика изобретения, логика воображения, не преуспела.
Возможно, здесь окажется полезной комбинаторная геометрия (а наша модель — одна из них), целью которой является поиск оптимальной комбинации некоторых элементов-фигур (подобный подход ранее использовал Эдвард де Боно). Модель хорошо отражает различные ситуации, например, существование конкурирующих теорий — несколько систем счисления, соответствующих данному набору фактов. Или появление факта, который невозможно собрать из известных строительных блоков. Здесь необходимо построить новую теорию — разложить знакомые фигуры на части и сложить их по-новому (соответственно, провести анализ и синтез).
Помимо чисто комбинаторных трудностей, еще одним препятствием является то, что после длительного использования каждая картина начинает восприниматься как неделимое целое, что связано с догматизмом мышления и бюрократизмом в его многочисленных проявлениях. Здесь, как правило, требуется свежий взгляд, которым часто обладает «чужак».
Конечно, «игра в кости» — это лишь иллюстрация некоторых способов мышления, и мы пока не можем говорить об универсальном подходе. И все же такая игра в какой-то мере иллюстрирует то, что Лейбниц мог иметь в виду, когда писал, что существует исчисление более важное, чем исчисление арифметики и геометрии, — исчисление идей.
Мозг создает, вероятно, еще неясным образом, связи и отношения между образами — энграммы памяти — и сам мыслительный процесс представляет собой перестройку этой структуры. Минимизация также работает в этом процессе — мы всегда ищем наиболее краткое представление вопроса; раньше это называлось принципом экономии мысли.
В целом, необходимость разработки «новой математики и логики» назрела давно. Как отмечали Джон фон Нейман и Людвиг фон Берталанфи, отцы кибернетики и теории систем, «логика должна будет претерпеть метаморфозу и превратиться в неврологию в гораздо большей степени, чем неврология превратится в ветвь логики», и «уже давно предпринимаются попытки создать «гештальт-математику», основанную не на количестве, а на отношениях, то есть на форме и порядке».
Компьютер может хранить любое количество информации (даже абсолютно бессмысленной) и выполнять миллионы действий с ней за секунду. Сначала надеялись, что эти достоинства уже гарантируют высокий интеллектуальный потенциал, но вскоре стало ясно, что большие знания не обязательно означают мудрость. Ведь, как мы видели, интеллект — это способность не отбрасывать плохие варианты, а находить хорошие, чего нельзя достичь примитивным перечислением.
Человек не запоминает большой объем неорганизованной информации (как телефонный справочник), но его знания хорошо структурированы и взаимосвязаны в его сознании. Они во многом отражают существенные страницы реальности: наборы маршрутных «карт» взаимосвязаны по вертикали и горизонтали, каждое понятие окружено своей «ассоциативной аурой» (Д.С.Лихачев). Такое богатство связей позволяет извлекать только релевантную информацию и уже на ее основе строить необходимое решение.
Необходимо оснастить компьютер знаниями о мире, моделью мира. Для этого вводится набор «сценариев». Сценарий — это общая рамка, стереотип, который каждый раз должен наполняться конкретным содержанием. Распознав ситуацию, машина находит подходящий сценарий, затем задает вопросы и сама уточняет недостающие детали.
Это нелегко, учитывая, что запас таких шаблонов у человека поистине колоссален — в них кристаллизуется опыт всей прожитой до сих пор жизни. Любое явление мы представляем себе во множестве сокращений и ракурсов, а некоторые вещи, например, пространственные отношения, мы бессознательно усваиваем в раннем детстве.
Нейронные сети и нейрокомпьютеры
В последнее время ведется активная работа по построению моделей обработки информации в нервной системе. Большинство моделей основано на схеме формального нейрона У. Маккаллоха и У. Питтса, согласно которой нейрон — это пороговый элемент, входы которого имеют возбуждающие и тормозные синапсы; в таком нейроне определяется взвешенная сумма входных сигналов (с учетом весов синапсов), и когда эта сумма превышает порог нейрона, формируется выходной сигнал.
В моделях уже построены нейронные сети, выполняющие различные алгоритмы обработки информации: ассоциативная память, категоризация (разбиение множества изображений на кластеры, состоящие из похожих друг на друга изображений), топологически корректное отображение одного пространства переменных в другое, распознавание зрительных образов, инвариантное при деформациях и смещениях в пространстве решение задач комбинаторной оптимизации. Подавляющее число работ связано с изучением нейросетевых алгоритмов с прагматическими целями.
Практические задачи должны решать нейрокомпьютеры — искусственные нейроподобные сети на основе микроэлектронных вычислительных систем. Спектр задач для разрабатываемых нейрокомпьютеров достаточно широк: распознавание визуальных и акустических образов, создание экспертных систем и их аналогов, управление роботами, создание нейронных протезов для людей, потерявших слух или зрение. Преимуществами нейрокомпьютеров являются параллельная обработка информации и способность к обучению.
Несмотря на необычайную активность в исследованиях нейронных сетей и нейрокомпьютеров, большая часть этих исследований вызывает тревогу. Действительно, изучаемые алгоритмы кажутся «оторванным куском» от общего понимания того, как работает нервная система. Алгоритмы, для которых нам удается построить хорошие модели, часто изучаются вместо тех, которые наиболее важны для понимания свойств мышления, работы мозга и создания систем искусственного интеллекта. Проблемы, решаемые этими алгоритмами, оторваны от эволюционного контекста; они практически не учитывают, как и почему возникли те или иные системы обработки информации. Также настораживает чрезмерное упрощение понимания нейронных сетей, в котором нейроны концептуализируются только как суммирующие пороговые элементы, а обучение сети происходит через модификацию синапсов. Однако ряд исследователей рассматривают нейрон как гораздо более сложную систему обработки информации и предполагают, что молекулярные механизмы в нейроне играют важную роль в обучении. Все это указывает на необходимость максимально полного понимания того, как работают биологические системы обработки информации и какие свойства организмов обеспечиваются этими системами. Важной областью исследований, которая могла бы способствовать такому пониманию, вероятно, был бы анализ того, как «разумные» свойства биологических организмов возникли в процессе биологической эволюции.
«Умственные изобретения» биологической эволюции
Интересно понять, как возникла человеческая логика в процессе биологической эволюции. Анализ связан с глубокой эпистемологической проблемой: почему человеческая логика применима к познанию природы? Давайте кратко объясним суть проблемы на простом примере. Предположим, что физику, изучающему динамику объекта, удалось свести его описание к дифференциальному уравнению в определенном приближении. Далее, разумеется, он интегрирует полученное уравнение по известным из математики правилам и таким образом получает свойства движения объекта. Переход от дифференциального уравнения к свойствам движения является дедуктивным, но, чтобы быть очень строгим, этот переход должен быть обоснован: физический объект не обязательно подчиняется правилам человеческой логики!
Для того чтобы понять происхождение логики, была предпринята попытка построить модельную теорию происхождения логики в биосфере. Такая теория может включать математические модели основных «интеллектуальных изобретений» биологической эволюции, подчеркивая как биологическое значение и причины появления этих изобретений, так и модели, описывающие переходы между изобретениями на разных уровнях. Самый надежный способ, по-видимому, заключается в том, чтобы начать с «начала» — зарождения жизни — и проследить весь путь биологической эволюции от простейших организмов до человека, подчеркивая по пути основные эволюционные открытия, которые приводят к логике. Чтобы проиллюстрировать круг вопросов, составляющих предмет модельной теории происхождения логики, отметим несколько важных уровней «интеллектуального изобретения».
Первый уровень — организм различает состояния внешней среды, память об этих состояниях записана в геноме и передается по наследству, организм адекватно использует разницу в средах и меняет свое поведение с изменением среды. Примером этого уровня является свойство регуляции синтеза белка у бактерий в ответ на изменение питательных веществ во внешней среде по схеме Ф. Жакоба и Ж. Моно. Это свойство можно назвать элементарной чувствительностью.
Второй уровень — это временная память организма о состоянии окружающей среды и соответствующая, тоже временная, адаптация к этому состоянию. Примером этого уровня является привыкание, а именно постепенное угасание стимульной реакции на биологически нейтральный стимул.
Третий уровень — это запечатление устойчивых связей между событиями в окружающей организм среде. Хорошим примером является классический условный рефлекс, изученный И. Павловым, в котором существует долговременная память на связь между обусловленными и необусловленными стимулами и подготовка к жизненно важным событиям во внешнем мире.
Между классическим условным рефлексом и логикой существует ряд промежуточных стадий. Например, инструментально обусловленный рефлекс отличается от классического тем, что для получения вознаграждения животное должно выполнить действие, ранее ему неизвестное. Цепь условных рефлексов — это система реакций, сформированных на основе условных связей, ранее хранившихся в памяти животного.
Изучение моделей «мысленных изобретений» биологической эволюции показывает их крайнюю фрагментарность и слабую проработанность. Не существует абсолютно никаких моделей переходов между «изобретениями» разных уровней. Сейчас мы можем лишь предварительно указать на некоторые аналогии. Например, выработку условного рефлекса можно рассматривать как элементарное умозаключение, возникающее в нервной системе животного — «если за условным стимулом следует безусловный, и безусловный стимул вызывает определенную реакцию, то и условный стимул вызывает эту реакцию» — отдаленный предшественник формул дедуктивной логики.
На странице рефераты по философии вы найдете много готовых тем для рефератов по предмету «Философия».
Читайте дополнительные лекции:
- Религиозное освоение мира. Специфика религиозного опыта
- Умопостижение: его пределы и методы
- Фрэнсис Бэкон
- Методология научного поиска: рационализм, эмпиризм, интуитивизм — Эмпиризм — опыт как единственный источник знаний
- Физическое и математическое моделирование
- В чем состоит значение философии сегодня
- Нравственный идеал – недостижимое, но необходимое условие индивидуального и общественного бытия
- Средневековая философия как синтез христианского учения и античной философии
- Людвиг Фейербах, немецкий философ
- Позитивизм

