Оглавление:
Мощность силы
Мощностью силы называется изменение ее работы за единицу времени
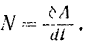
Мощность силы в момент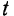 
равна отношению элементарной работы 
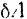силы за бесконечно малый промежуток времени 
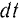, начинающийся в момент 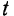к величине 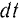этого промежутка времени. Подставляя в формулу (197) значение элементарной работы, получим:
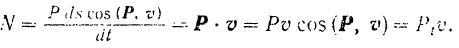
Мощность силы в данный момент равна произведению модуля касательной составляющей силы на модуль скорости ее точки приложения.
Если в данный момент времени направление силы совпадает с направлением скорости ее точки приложения, то
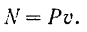
Размерность мощности определяется равенством
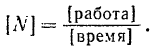
Так как в технической системе единиц работа измеряется в килограммометрах, а время — в секундах, то мощность в технической системе измеряется в килограммометрах в секунду (кГм/сек).
Вследствие малости данной единицы, в технической практике часто еще пользуются более крупной единицей мощности, называемой лошадиной силой (л. с.):
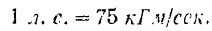
В системе СИ работа измеряется в джоулях и время в секундах, поэтому мощность в этой системе измеряется в джоулях а секунду (дж/сек).
Мощность, равная и джоулю в 1 секунду, называется ваттом (вт.)
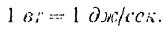
Найдем соотношение между лошадиной силой и ваттом. Ранее (стр. 339) было установлено, что 1 кГм— — 9,81 дж. Следовательно,
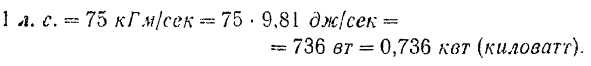
Пример задачи:
Для использования работы водопада поставлена турбина, коэффициент полезною действия (к. п. д.) которой
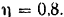
Определить о киловаттах полезную мощность турбины, если водопад дает в точение каждой минуты 600 м воды, падающей с высоты 6 м.
Решение:
Масса I куб. метра воды равна 1000 кг. Вес воды, падающей в течение одной минуты.
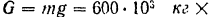
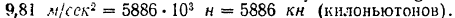
По формуле (199) потребляемая турбиной мощность будет равна
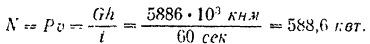
Следовательно, полезная мощность турбины
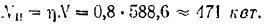
Пример задачи:
Каким должен быть диаметр поршня одноцилиндровой паровой машины при среднем давлении пара на поршень
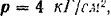
средней скорости поршня
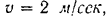
полезной мощности машины
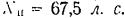
и ее механическом к. п. д.
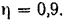
Решение:
Потребляемая машиной мощность пара
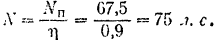
Так как направление давления пара на поршень совпадает с направлением его движения, то по формуле (199) мощность, выраженная в лошадиных силах, будет
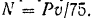
Отсюда сила, с которой пар давит на поршень,
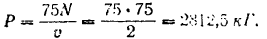
С другой стороны, эта сила равна удельному давлению пара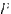 
умноженному на площадь поршня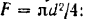 
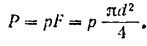
Следовательно, диаметр поршня должен быть равным:
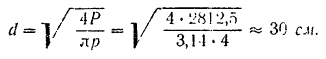
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
