Оглавление:
Определение 1. Функция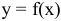 
называется возрастающей в интервале 
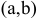, если большему значению аргумента 
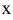из этого интервала соответствует и большее значение функции.
Определение 2. Функция 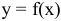называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Достаточное условие возрастания ( убывания ) функции:
Если во всех точках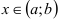 
выполняется неравенство 
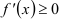(причем равенство 
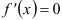выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке), то функция 
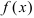возрастает в интервале 
.
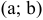Если в данном промежутке производная данной функции неотрицательна, то функция в этом промежутке убывает.
Справедливы и обратные утверждения.
Определение 3. Максимумом функции 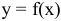такое ее значение 
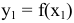, которое больше всех ее значений, принимаемых в точках 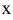, достаточно близких к точке 
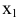и отличных от нее, т. е. 
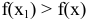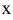, где — любая точка из интервала, содержащего точку 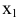( 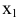— точка максимума ).
Определение 4. Минимумом функции 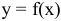называется такое ее значение 
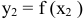, которое меньше всех других ее значений, принимаемых в точках 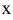, достаточно близких к точке 
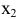и отличных от нее, т. е. 
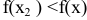, где 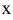— любая точка из некоторого интервала, содержащего точку 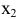( 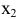— точка минимума).
Максимум или минимум функции называется экстремумом функции. Точки, в которых достигается экстремум, называются точками экстремума.
Функция может иметь экстремум в тех точках области определения, в которых производная равна нулю или не существует . Такие точки называются критическими .
Достаточное условие экстремума
Если в точке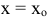 
производная функции 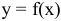обращается в нуль или не существует, и меняет знак при переходе через эту точку, то 
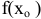— экстремум функции, причем:
1) функция имеет максимум в точке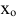 
, если знак производной меняется с «+» на «-»;
2) функция имеет минимум в точке 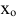, если знак производной меняется с «-» на «+»%
3) функция не имеет экстремума, если знак производной не меняется.
Алгоритм исследования непрерывной функции 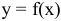на монотонность и экстремумы.
- Найти область определения и производную
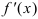. - Найти критические точки.
- Отметить критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
- Опираясь на теоремы сделать выводы о монотонности и о ее точках экстремума.
Пример:
Исследовать функцию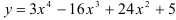 
на монотонность и экстремумы.
Решение:
1. Найдем область определения: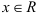 
и производную данной функции:
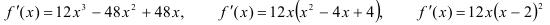
2. Найдем критические точки.
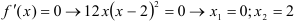— это две критические точки.
3. Отметим полученные точки на числовой прямой и схематически укажем знаки производной по промежуткам области определения.
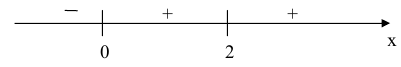
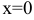— точка минимума функции, а 
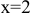точкой экстремума не является.
На промежутке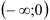 
функция убывает, а на промежутке 
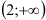функция возрастает.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
