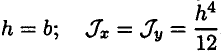Моменты инерции простейших сечений
Осевые моменты инерции прямоугольника (рис. 25.2)
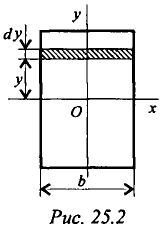
Представим прямоугольник высотой 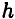 и шириной
и шириной 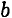 в виде сечения, составленного из бесконечно тонких полос. Запишем площадь такой полосы
в виде сечения, составленного из бесконечно тонких полос. Запишем площадь такой полосы 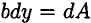 . Подставим в формулу осевого момента инерции относительно оси
. Подставим в формулу осевого момента инерции относительно оси 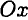 :
:
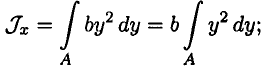
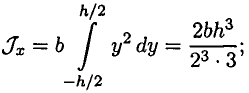
получим:
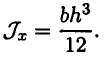
По аналогии, если разбить прямоугольник на вертикальные полосы, рассчитать площади полос и подставить в формулу для осевого момента инерции относительно оси 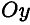 , получим:
, получим:
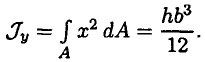
Очевидно, что при 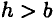 сопротивление повороту относительно оси
сопротивление повороту относительно оси 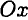 больше, чем относительно
больше, чем относительно 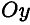 .
.
Для квадрата: