Оглавление:
Моменты инерции некоторых однородных тел простейшей формы относительно их центральных осей симметрии
Момент инерции тонкого прямого стержня постоянного сечения
Продольную ось симметрии стержня длиной 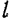 (рис. 182) примем за ось
(рис. 182) примем за ось 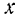 .
.
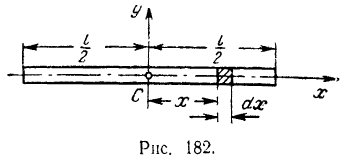
Массу одного элементарного отрезка стержня длиною 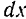 , отстоящего, от центральной оси
, отстоящего, от центральной оси 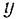 на расстоянии
на расстоянии 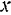 , обозначим через
, обозначим через 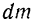 . Если обозначить линейную плотность стержня через
. Если обозначить линейную плотность стержня через 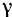 , то масса элемента длины стержня
, то масса элемента длины стержня 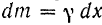 .
.
Составляя в соответствии с определением понятия момента инерции тела относительно оси сумму из произведений массы каждого элемента длины стержня па квадрат ее расстояния до оси 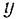 и переходя к пределу, получим определенный интеграл:
и переходя к пределу, получим определенный интеграл:
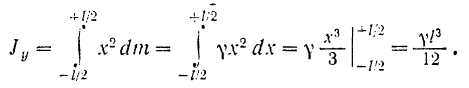
Если обозначить массу всего стержня через 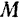 , то
, то 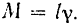 . Подставляя значение линейной плотности
. Подставляя значение линейной плотности 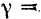
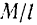 в предыдущее равенство, окончательно получаем
в предыдущее равенство, окончательно получаем
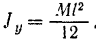
Момент инерции однородного прямого тонкого стержня относительно его центральной оси симметрии равен 1/12 произведения массы стержня на квадрат его длины.
Момент инерции сплошного круглого цилиндра
Разобьем цилиндр радиуса 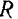 и высоты
и высоты 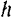 (рис. 183) на бесконечно тонкие цилиндрические слои. Массу одного такого цилиндрического слоя радиуса
(рис. 183) на бесконечно тонкие цилиндрические слои. Массу одного такого цилиндрического слоя радиуса 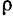 и толщины
и толщины 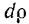 обозначим через
обозначим через 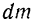 .
.
Обозначим плотность цилиндра через 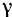 Тогда
Тогда 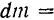
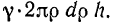 Составляя сумму из произведений массы каждого слоя цилиндра на квадрат его расстояния до оси, получим:
Составляя сумму из произведений массы каждого слоя цилиндра на квадрат его расстояния до оси, получим:
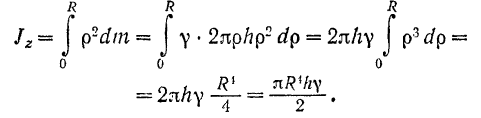
Если обозначить массу всего цилиндра через 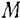 , то эта масса
, то эта масса
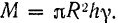
Отсюда плотность цилиндра
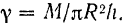
Подставляя это значение плотности в найденное выражение момента инерции цилиндра, окончательно получаем:
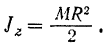
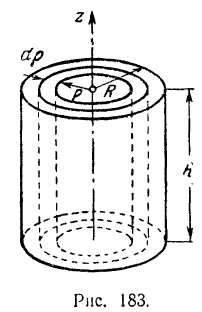
Момент инерции однородного сплошного круглого цилиндра относительно его оси вращения равен половине произведения массы цилиндра на квадрат его радиуса.
Момент инерции полого круглого цилиндра
Обозначим наружный радиус полого цилиндра через 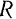 и его внутренний радиус — через
и его внутренний радиус — через 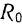 . Разбивая полый цилиндр на бесконечно тонкие цилиндрические слои, мы придем, очевидно, к тому же самому определенному интегралу, что и в предыдущем случае, только с другими пределами интегрирования. Пределы интегрирования будут изменяться не от нуля до
. Разбивая полый цилиндр на бесконечно тонкие цилиндрические слои, мы придем, очевидно, к тому же самому определенному интегралу, что и в предыдущем случае, только с другими пределами интегрирования. Пределы интегрирования будут изменяться не от нуля до 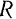 , а только от
, а только от 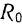 до
до 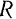 . Следовательно,
. Следовательно,
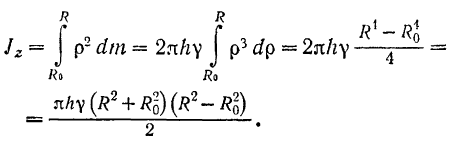
Масса же полого цилиндра
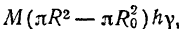
откуда находим плотность цилиндра
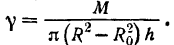
Подставляя это значение плотности в найденное выражение момента инерции полого цилиндра относительно его оси вращения, окончательно получаем:
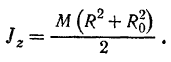
Момент инерции однородного полого круглого цилиндра относительно его оси вращения равен половине произведения массы цилиндра ‘на сумму квадратов его наружного и внутреннего радиусов.
Момент инерции тела имеет следующую размерность:
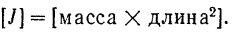
В системе СИ момент инерции измеряется в 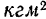 . В технической системе единица массы является производной единицей и момент инерции имеет размерность
. В технической системе единица массы является производной единицей и момент инерции имеет размерность
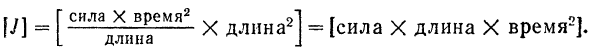
Следовательно, в технической системе единиц момент инерции измеряется в 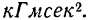 .
.
Формулы для определения моментов инерции однородных тел различной геометрической формы можно найти в технических справочниках.
Для тел неоднородных или имеющих сложное очертание моменты инерции обычно находятся экспериментальным путем.
Пример задачи:
Определить радиус инерции однородного тонкого стержня относительно оси 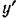 , перпендикулярной к стержню и проходящей через его конец.
, перпендикулярной к стержню и проходящей через его конец.
Решение:
По теореме о моментах инерции относительно параллельных осей (формула (143))
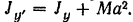
Момент инерции стержня относительно его центральной оси симметрии вычисляем по формуле (144):
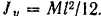
Расстояние между параллельными осями 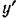 и
и 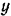 равно
равно
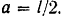
Следовательно,
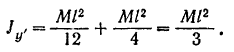
Искомый радиус инерции стержня определяется по формуле (142);
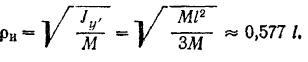
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Момент инерции тела относительно оси |
| Теорема о моментах инерции тела относительно параллельных осей |
| Об основных теоремах динамики |
| Количество движения точки и системы |

